
题目列表(包括答案和解析)
 如图,在△BCD中,∠BDC=90°,以BD为斜边,向外作Rt△ABD.若AD=4,∠ADB=∠C.且P是BC边上一动点,则DP长的最小值为
如图,在△BCD中,∠BDC=90°,以BD为斜边,向外作Rt△ABD.若AD=4,∠ADB=∠C.且P是BC边上一动点,则DP长的最小值为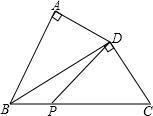 如图,在△BCD中,∠BDC=90°,以BD为斜边,向外作Rt△ABD.若AD=4,∠ADB=∠C.且P是BC边上一动点,则DP长的最小值为________.
如图,在△BCD中,∠BDC=90°,以BD为斜边,向外作Rt△ABD.若AD=4,∠ADB=∠C.且P是BC边上一动点,则DP长的最小值为________. 24、先阅读下面的材料,然后解答问题:
24、先阅读下面的材料,然后解答问题:
 先阅读下面的材料,然后解答问题:
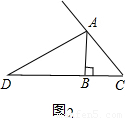
先阅读下面的材料,然后解答问题: 如图2”,其他条件不变,请你猜想线段AC、AB、BD之间的数量关系,并证明你的猜想.
如图2”,其他条件不变,请你猜想线段AC、AB、BD之间的数量关系,并证明你的猜想.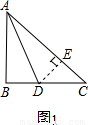
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com