填空并完成推理过程.
(1)如图(1),∵AB∥EF,(已知)
∴∠A+
∠AEF
∠AEF
=180°.(
两直线平行,同旁内角互补
两直线平行,同旁内角互补
)
∵DE∥BC,(已知)
∴∠DEF=
∠CFE
∠CFE
,(
两直线平行,内错角相等
两直线平行,内错角相等
)∠ADE=
∠B
∠B
;(
两直线平行,同位角相等
两直线平行,同位角相等
)
(2)如图(2),已知AB⊥BC,BC⊥CD,∠1=∠2.试判断BE与CF的关系,并说明你的理由.
解:BE∥CF,理由是:∵AB⊥BC,BC⊥CD.(已知)
∴
∠ABC
∠ABC
=
∠BCD
∠BCD
=90°.(
垂直定义
垂直定义
)
∵∠1=∠2,(
已知
已知
)
∴∠ABC-∠1=∠BCD-∠2,即∠EBC=∠BCF.
∴
BE
BE
∥
CF
CF
;(
内错角相等,两直线平行
内错角相等,两直线平行
)
(3)如图(3),E点为DF上的点,B点为AC上的点,∠1=∠2,∠C=∠D,试说明:AC∥DF.
解:∵∠1=∠2,(已知)∠1=∠3,(
对顶角相等
对顶角相等
)
∴∠2=∠3,(等量代换)
∴
BD
BD
∥
CE
CE
,(
同位角相等,两直线平行
同位角相等,两直线平行
)
∴∠C=∠ABD,(
两直线平行,同位角相等
两直线平行,同位角相等
)
又∵∠C=∠D,(已知)
∴∠D=∠ABD,(
等量代换
等量代换
)
∴AC∥DF.(
内错角相等,两直线平行
内错角相等,两直线平行
)


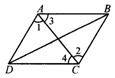 3、如图,按要求填空.
3、如图,按要求填空.
 如图:填空
如图:填空 填空题:如图,AB∥CD,∠ABC=50°,∠CPN=150°,∠PNB=60°,∠NDC=60°,求∠BCP的度数.
填空题:如图,AB∥CD,∠ABC=50°,∠CPN=150°,∠PNB=60°,∠NDC=60°,求∠BCP的度数.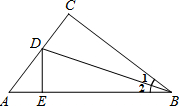 填空,完成下列说理过程.
填空,完成下列说理过程.