打市内电话都按时收费，并于200l年3月21日起对收费办法作了调整，调整前的收费办法：以3分钟为计时单位（不足3分钟按3分钟计），每个计时单位收0.2元；调整后的收费办法：3分钟内（含3分钟）0.2元，以后每加1分钟加收0.1元。

（1）根据调整后的收费办法，求电话费y（元）与通话时间t（分）之间的函数关系式（t＞3时设t（分）表示正整数）。

①当t3时，y=                ；

②当t＞3时（t（分）表示正整数），y=                     。

（2）就0＜t6，求t为何值时，调整前和调整后的电话费相同，并求出其相应的收费y（元）。

某地各城镇打市内电话都按时间收费，2003年3月21日起对收费作了调整，调整前的收费方法为：以3分为计时单位(不足3分按3分计)，每个计时单位收0.2元；调整后的收费方法为：3分内(含3分)收0.2元，以后每加1分加收0.1元．

①根据调整后的收费方法，求电话费y(元)与通话时间t(分)之间的函数关系式(t＞3时，且t表示正整数)；

②对①中，试画出0＜t≤6时，函数的图象；

③就0＜t≤6，求t为何值时，调整前和调整后的电话费相同，并求其相应的收费y(元)．

某地各城镇打市内电话都按时间收费，2003年3月21日起对收费作了调整，调整前的收费方法为：以3分为计时单位(不足3分按3分计)，每个计时单位收0.2元；调整后的收费方法为：3分内(含3分)收0.2元，以后每加1分加收0.1元．

①根据调整后的收费方法，求电话费y(元)与通话时间x(分)之间的函数关系式(t＞3时，且t表示正整数)；

②对①中，试画出0＜t≤6时，函数的图象；

③就0＜t≤6，求t为何值时，调整前和调整后的电话费相同，并求其相应的收费y(元)．

某市各城镇打市内电话都按时间收费，并于2001年3月21日起对收费作了

调整。调整前的收费方法是以3分钟为计时单位（不足3分钟按3分钟计），每个计时

单位收0.2元；调整后的收费方法是3分钟内（含3分钟）收0.2元，以后每加1分钟

加收0.1元。

（1）根据调整后的收费方法，求电话费y（元）与通话时间t（min）之间的函数关系

式［t＞3时，设t（min）表示正整数］；

（2）对（1）试画出3＜t≤6时函数的图象；

（3）若0＜t≤6，求t为何值时，调整前和调整后的电话费相同，并求其相应的收费y

（元）。

 

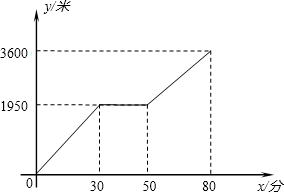小颖和小亮上山游玩，小颖乘坐缆车，小亮步行，两人相约在山顶的缆车终点会合．已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍，小颖在小亮出发后50 分才乘上缆车，缆车的平均速度为180米/分．设小亮出发x 分后行走的路程为y 米．图中的折线表示小亮在整个行走过程中y随x的变化关系．
（1）小亮行走的总路程是米，他途中休息了分．
（2）分别求出小亮在休息前和休息后所走的路程段上的步行速度．
（3）当小颖到达缆车终点时，小亮离缆车终点的路程是多少？