
题目列表(包括答案和解析)
| x | 2 |
| x | 2 |
| y | 2 |
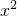 -9=______;
-9=______;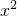 -2xy+
-2xy+ =______.
=______.下面是某同学对多项式(x2—4x+2)(x2—4x+6)+4进行分解因式的过程。
解:设x2—4x=y.
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2 (第三步)
=(x2—4x+4)2 (第四步)
回答下列问题:
(1)该同学第二步到第三步运用了分解因式的 ;
A.提取公因式 B.逆用平方差公式 C.逆用完全平方公式
(2)该同学分解因式的结果不正确,应更正为 ;
(3)试分解因式n(n+1)(n+2)(n+3)+1.
下面是某同学对多项式(x2—4x+2)(x2—4x+6)+4进行分解因式的过程。
解:设x2—4x=y.
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2 (第三步)
=(x2—4x+4)2 (第四步)
回答下列问题:
(1)该同学第二步到第三步运用了分解因式的 ;
A.提取公因式 B.逆用平方差公式 C.逆用完全平方公式
(2)该同学分解因式的结果不正确,应更正为 ;
(3)试分解因式n(n+1)(n+2)(n+3)+1.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com