
题目列表(包括答案和解析)
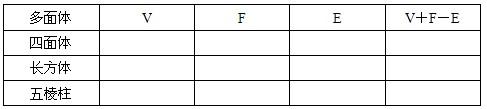
| 多面体 | V | F | E | V+F-E |
| 四面体 | ||||
| 长方体 | ||||
| 五棱柱 |
两袋分别装着写有0、1、2、3、4、5六个数字的六张卡片,从每袋中各取一张,求所得两数之和等于6的概率.现在小华和小晶给出下述两种不同解答:
小华的解法:两数之和共有0,1,2,…,10,十一种不同结果,因此所求的概率是![]() .
.
小晶的解法:从每袋中各任取一张卡片,共有36种取法,其中和数为6的情形共有5种:(1,5),(2,4),(3,3),(4,2),(5,1),因此所求的概率为![]() ,试问哪一种解法正确,为什么?
,试问哪一种解法正确,为什么?
在计算器上依次按键:![]() 、25、=,此时所得的结果是
、25、=,此时所得的结果是
25
2.924
5
10

| 2 |
| 105 |
| 3 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com