
题目列表(包括答案和解析)
如图所示,要剪切如图(1)所示(尺寸单位:mm)的甲、乙两种直角梯形零件,且使两种零件的数量相等,有两种面积相等的矩形铝板,第一种长500mm,宽300mm(如图(2)所示);第二种长600mm,宽250mrn(如图(3)所示)可供选用.(1)填空:为了充分利用材料,应选用第________种铝板,这时一块铝板最多能剪甲、乙两种零件共________个,剪下这些零件后,剩余的边角料的面积是________mm2.
(2)画图:从图(2)或图(3)中选出代要用的铝板示意图,从图上面画出剪切线,并把边角余料用阴影表示出来.

| 3 |
| 3 |


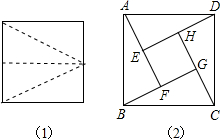 将一个面积为7的正方形分割成如图1所示的四个形状相同、大小相等的直角三角形,再将这四个直角三角形拼成如图2所示的正方形ABCD,其中四边形EFGH也是正方形,求正方形ABCD的面积.
将一个面积为7的正方形分割成如图1所示的四个形状相同、大小相等的直角三角形,再将这四个直角三角形拼成如图2所示的正方形ABCD,其中四边形EFGH也是正方形,求正方形ABCD的面积.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com