
题目列表(包括答案和解析)
 在一张纸上画两个全等的直角三角形,并把它们拼成如图形状,请用两种方法表示这个梯形的面积.利用你的表示方法,你能得到勾股定理吗?
在一张纸上画两个全等的直角三角形,并把它们拼成如图形状,请用两种方法表示这个梯形的面积.利用你的表示方法,你能得到勾股定理吗?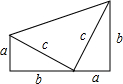 在一张纸上画两个全等的直角三角形,并把它们拼成如图形状,请用两种方法表示这个梯形的面积.利用你的表示方法,你能得到勾股定理吗?
在一张纸上画两个全等的直角三角形,并把它们拼成如图形状,请用两种方法表示这个梯形的面积.利用你的表示方法,你能得到勾股定理吗?如图,正方形表示一张纸片,根据要求,需通过多次分割,将正方形纸片分割成若干个直角三角形,操作过程如下:第一次分割,将正方形纸片分成4个全等的直角三角形;第二次分割,将上次得到的直角三角形中的一个再分成4个全等直角三角形;以后按第二次分割的做法进行下去.
(1)请你设计出两种符合题意的分割方案图(要求在图1、图2中分别画出每种方案的第一次和第二次的分割线,只要有一条分割线段不同,就视为一种不同方案,图3供操作、实验用).

(2)设正方形的边长为a,请你就其中一种方案通过操作和观察将第二、第三次分割后所得的最小直角三角形的面积S填入下表:

(3)在条件(2)下,请你猜想:分割所得的最小直角三角形的面积S与分割次数n有什么关系?用数学表达式表示出来.
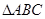 折叠,使点
折叠,使点 与点
与点 重合,这时
重合,这时 为折痕,
为折痕, 为等腰三角形;再继续将纸片沿
为等腰三角形;再继续将纸片沿 的对称轴
的对称轴 折叠,这时得到了两个完全重合的矩形(其中一个是原直角三角形的内接矩形,另一个是拼合成的无缝隙、无重叠的矩形),我们称这样两个矩形为“叠加矩形”.
折叠,这时得到了两个完全重合的矩形(其中一个是原直角三角形的内接矩形,另一个是拼合成的无缝隙、无重叠的矩形),我们称这样两个矩形为“叠加矩形”.
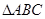 能折叠成“叠加矩形”吗?如果能,请在图②中画出折痕;
能折叠成“叠加矩形”吗?如果能,请在图②中画出折痕; 为一边,画出一个斜三角形
为一边,画出一个斜三角形 ,使其顶点
,使其顶点 在格点上,且
在格点上,且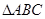 折成的“叠加矩形”为正方形;
折成的“叠加矩形”为正方形;如图所示,有两种形状不同的直角三角形纸片各两块,其中一种纸片的两条直角边长分别为1和2,另一种纸片的两条直角边长都为2.图a、图b、图c是三张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1.请用三种方法将图中所给四块直角三角形纸片拼成平行四边形(非矩形),每种方法要把图中所给的四块直角三角形纸片全部用上,互不重叠且不留空隙,三种方法所拼得的平行四边形(非矩形)的周长互不相等,并把你所拼得的图形按实际大小画在图a、图b、图c的方格纸上.

要求:(1)所画图形各顶点必须与方格纸中的小正方形顶点重合.
(2)画图时,要保留四块直角三角形纸片的拼接痕迹.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com