
题目列表(包括答案和解析)
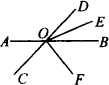
如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE,∠AOD∶∠BOE=4∶1,求∠AOF的度数.[方法提示:先由∠AOD∶∠BOE=4∶1及∠BOE=∠EOD和邻补角可求出∠BOE=30°,∠AOD=120°,再求∠COF.]
如图,在△ABC中,AB=BC=26cm,∠ABC=84°,BD是∠ABC的平分线,DE∥BC.
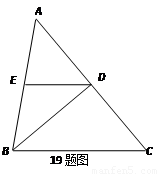
(1)求∠EDB的度数;
(2)求DE的长.
【解析】(1)根据平行线及角平分线的性质可求出∠EDB的度数;
(2)根据三角形中位线定理可求出DE的长.
如图,已知,△ABC中,BD、CE分别是△ABC两条角平分线,相交于点O.

(1)当∠ABC=![]() 时,∠ACB=
时,∠ACB=![]() 时,∠ABC+∠ACB=
时,∠ABC+∠ACB=![]() ,
,![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() ,∠BOC=
,∠BOC=![]() .
.
(2)当∠A=![]() 时,∠ABC+∠ACB=
时,∠ABC+∠ACB=![]() ,
,![]() (∠ACB+∠ABC)=
(∠ACB+∠ABC)=![]() ,∠BOC=
,∠BOC=![]() .
.
(3)当∠A=![]() 时,
时,![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() ,∠BOC=
,∠BOC=![]() .
.
(4)从上述计算过程中,我们能得到∠BOC与∠A的关系式为∠BOC=![]() ,若∠A=
,若∠A=![]() 时,应用上面公式可知∠BOC=
时,应用上面公式可知∠BOC=![]() ,若∠BOC=
,若∠BOC=![]() ,则可求出∠A=
,则可求出∠A=![]() .
.
 |
| AM |
 |
| MC |

| A、1个 | B、2个 | C、3个 | D、4个 |
 sA=
sA=| AD |
| b |
| 3 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com