阅读下面材料并填空：
已知点A、B在数轴上分别表示有理数a、b，A、B两点之间的距离表示为|AB|．当A、B两点中有一点在原点时，不妨设点A在原点，如图1，|AB|=|OB|=|b|=|a-b|，当A、B两点都不在原点时，
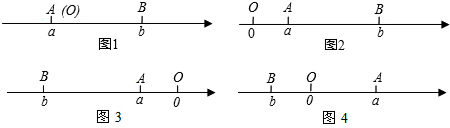
（1）如图2，点A、B都在原点的右边，|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|；
（2）如图3，点A、B在原点的左边，|AB|=|OB|-|OA|=|b|-|a|=-b-（-a）=a-b=|a-b|；
（3）如图4，点A、B在原点的两边，|AB|=|OA|+|OB|=|a|+|b|=a+（-b）=a-b=|a-b|．
综上，数轴上A、B两点的距离|AB|=|a-b|．
利用上述结论，小明同学这样解决了以下问题：
数轴上表示x和-1的两点之间的距离是|x+1|，表示x和2的两点之间的距离是|x-2|，当x的取值范围为-1≤x≤2时，代数式|x+1|+|x-2|取最小值3．并且他发现：对于代数式|x-a
1|+|x-a
2|+…+|x-a
n|，当n为奇数时，把a
1，a
2，…a
n从小到大排列，x等于最中间的数值时，原式值最小；当n为偶数时，把a
1，a
2，…a
n从小到大排列，x取最中间两个数值之间的数（包括最中间的两个数）时，原式值最小．
请你仿照小明的方法解决下面问题（也可以考虑其他方法）：
若y=|1-x|+|2-3x|+|3-4x|+|4-5x|+|5-6x|+|6-7x|，则当x的取值范围是
时，y取最小值
．
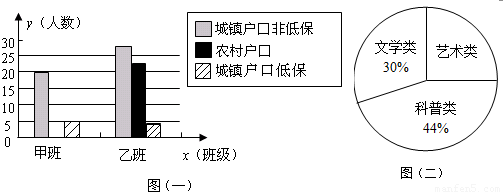
，城镇户口（非低保）学生全额交费．求乙班应交书费多少元？甲班受到国家资助教科书的学生占全班人数的百分比是多少？
，城镇户口（非低保）学生全额交费．求乙班应交书费多少元？甲班受到国家资助教科书的学生占全班人数的百分比是多少？
