
题目列表(包括答案和解析)
 如图,在直角△ABC中,∠ACB=90°,∠A=30°,以直角顶点C为旋转中心,将△ABC旋转到△A′B′C 的位置,其中A′、B′分别是A、B的对应点,且点B在斜边A′B′上,直角边CA′交AB于点D,这时∠BDC的度数是( )
如图,在直角△ABC中,∠ACB=90°,∠A=30°,以直角顶点C为旋转中心,将△ABC旋转到△A′B′C 的位置,其中A′、B′分别是A、B的对应点,且点B在斜边A′B′上,直角边CA′交AB于点D,这时∠BDC的度数是( )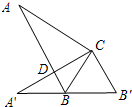 如图,在直角△ABC中,∠ACB=90°,∠A=30°,以直角顶点C为旋转中心,将△ABC旋转到△A′B′C 的位置,其中A′、B′分别是A、B的对应点,且点B在斜边A′B′上,直角边CA′交AB于点D,这时∠BDC的度数是
如图,在直角△ABC中,∠ACB=90°,∠A=30°,以直角顶点C为旋转中心,将△ABC旋转到△A′B′C 的位置,其中A′、B′分别是A、B的对应点,且点B在斜边A′B′上,直角边CA′交AB于点D,这时∠BDC的度数是如图,在直角△ABC中,∠C=![]() ,∠A=
,∠A=![]() ,以直角顶点C为旋转中心,将△ABC旋转到△
,以直角顶点C为旋转中心,将△ABC旋转到△![]() 的位置,其中
的位置,其中![]() 、
、![]() 分别是A、B的对应点,且点B在斜边
分别是A、B的对应点,且点B在斜边![]() 上,直角边
上,直角边![]() 交AB于D,求∠BDC的度数.
交AB于D,求∠BDC的度数.

如图所示,在Rt△ABC中,∠C=90°,∠BAC=60°,AB=8.半径为![]() 的⊙M与射线BA相切,切点为N,且AN=3.将Rt△ABC顺时针旋转120°后得到Rt△ADE,点B、C的对应点分别是点D、E.
的⊙M与射线BA相切,切点为N,且AN=3.将Rt△ABC顺时针旋转120°后得到Rt△ADE,点B、C的对应点分别是点D、E.

(1)画出旋转后的Rt△ADE;
(2)求出Rt△ADE的直角边DE被⊙M截得的弦PQ的长度;
(3)判断Rt△ADE的斜边AD所在的直线与⊙M的位置关系,并说明理由.
在图1中,正方形ABCD的边长为a,等腰直角三角形FAE的斜边AE=2b,且边AD和AE在同一直线上.
操作示例
当2b<a时,如图1,在BA上选取点G,使BG=b,连结FG和CG,裁掉△FAG和△CGB并分别拼接到△FEH和△CHD的位置构成四边形FGCH.
思考发现
小明在操作后发现:该剪拼方法就是先将△FAG绕点F逆时针旋转90°到△FEH的位置,易知EH与AD在同一直线上.连结CH,由剪拼方法可得DH=BG,故△CHD≌△CGB,从而又可将△CGB绕点C顺时针旋转90°到△CHD的位置.这样,对于剪拼得到的四边形FGCH(如图1),过点F作FM⊥AE于点M(图略),利用SAS公理可判断△HFM≌△CHD,易得FH=HC=GC=FG,∠FHC=90°.进而根据正方形的判定方法,可以判断出四边形FGCH是正方形.
实践探究
1.正方形FGCH的面积是 ;(用含a, b的式子表示)
2.类比图1的剪拼方法,请你就图2—图4的三种情形分别画出剪拼成一个新正方形的示意图.


3.联想拓展小明通过探究后发现:当b≤a时,此类图形都能剪拼成正方形,且所选取的点G的位置在BA方向上随着b的增大不断上移.当b>a时(如图5),能否剪拼成一个正方形?若能,请你在图5中画出剪拼成的正方形的示意图;若不能,简要说明理由.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com