练习册

  • 练习册
  • 试题
    函数y＝的自变量x的取值范围是 [ ] A.x≥3 B.x≠3 C.x＞3 D.x＜3 【查看更多】

     

    题目列表(包括答案和解析)

    如图所示，甲乙两船分别从相距100海里的A，B两地同时出发，甲船以10海里／时的速度沿AB向正西方向行驶，乙船以20海里／时的速度向正南方向行驶，直到甲船到达B点为止，设经过t小时后，两船距离的平方为y．

    (1)

    用函数表达式表示：y＝________

    (2)

    用表格表示：

    (3)

    在图中作出图象表示：

    (4)

    在这个问题中，自变量t的取值范围是________；图象的对称轴是________，顶点坐标是________：当t＜________时，y的值随t的值增大而________，当t＞________时，y的值随t的值增大而________(填“增大”或“减小”)；当t________时，y取得最小值为________

    查看答案和解析>>

    已知：关于x的一元二次方程mx2-(3m+2)x+2m+2=0(m＞0)，

        (1)求证：方程有两个不相等的实数根；

        (2)设方程的两个实数根分别为x1，x2(其中x1＜x2＝，若y是关于m的函数，且y=x2-2x1，求这个函数的解析式；

        (3)在(2)的条件下，结合函数的图象回答：当自变量m的取值范围满足什么条件时，y≤2m．

    查看答案和解析>>

    已知：关于x的一元二次方程mx2－(3m＋2)x＋2m＋2＝0(m＞0)．

    (1)求证：方程有两个不相等的实数根；

    (2)设方程的两个实数根分别为x1，x2(其中x1＜x2)．若y是关于m的函数，且y＝x2－2x1，求这个函数的解析式；

    (3)在(2)的条件下，结合函数的图象回答：当自变量m的取值范围满足什么条件时，y≤2m．

    查看答案和解析>>

    直线y＝kx＋b(k≠0)与坐标轴分别交于A、B两点，OA、OB的长分别是方程x2－14x＋48＝0的两根(OA＞OB)，动点P从O点出发，沿路线O→B→A以每秒1个单位长度的速度运动，到达A点时运动停止．

    (1)直接写出A、B两点的坐标；

    (2)设点P的运动时间为t(秒)，△OPA的面积为S，求S与t之间的函数关系式(不必写出自变量的取值范围)；

    (3)当S＝12时，直接写出点P的坐标，此时，在坐标轴上是否存在点M，使以O、A、P、M为顶点的四边形是梯形？若存在，请直接写出点M的坐标；若不存在，请说明理由．

    查看答案和解析>>

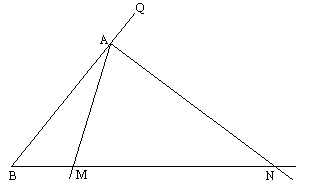
    如图，已知A为∠POQ的边OQ上一点，以A为顶点的∠MAN的两边分别交OP于M、N两点，且∠MAN＝∠POQ＝α(α为锐角)．当∠MAN以点A为旋转点中心，AM边从与AO重合的位置开始，按逆时针方向旋转(∠MAN保持不变)时，M、N在射线OP上同时以不同的速度向右平行移动．设OM＝x，ON＝y(y＞x≥0)，△AOM面积为S，若cosα、OA是方程2z2－5z＋2＝0的两个根．

    (1)当∠AMN旋转(即∠OAM＝)时，求点N移动的距离；

    (2)求证：AN2＝ON·MN；

    (3)求y与x之间的函数关系式及自变量x的取值范围；

    (4)试写出S随x变化的函数关系式，并确定S的取值范围．

    查看答案和解析>>


    同步练习册答案