
题目列表(包括答案和解析)
(本小题满分12分)
如图甲,在△ABC中,∠ACB为锐角.点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.
(1)如果AB=AC,∠BAC=90º.
解答下列问题:
①当点D在线段BC上时(与点B不重合),如图甲,线段CF、BD之间的位置关系为 ,数量关系为 .
②当点D在线段BC的延长线上时,如图乙,①中的结论是否仍然成立,为什么?(要求写出证明过程)
(2)如果AB≠AC,∠BAC≠90°,点D在线段BC上运动.且∠BCA=45°时,如图丙请你判断线段CF、BD之间的位置关系,并说明理由(要求写出证明过程).
(本小题满分12分)
某县有着丰富的海产品资源. 某海产品加工企业已收购某种海产品60吨, 根据市场信息, 如果对该海产品进行粗加工, 每天可加工8吨, 每吨可获利1000元;如果进行精加工,每天可加工2吨, 每吨可获利5000元. 由于受设备条件的限制,两种加工方式不能同时进行.
1.(1)设精加工的吨数为![]() 吨, 则粗加工的吨数为 吨,加工这批海产品需要 天, 可获利 元(用含
吨, 则粗加工的吨数为 吨,加工这批海产品需要 天, 可获利 元(用含![]() 的代数式表示);
的代数式表示);
2.(2)为了保鲜的需要, 该企业必须在两周(14天)内将这批海产品全部加工完毕,精加工的吨数![]() 在什么范围内时, 该企业加工这批海产品的获利不低于120000元?
在什么范围内时, 该企业加工这批海产品的获利不低于120000元?
(本小题满分12分)你还记得图形的旋转吗?如图,P是正方形ABCD内一点,
PA=a,PB=2a,PC=3a.将△APB绕点B按顺时针方向旋转,使AB与BC重合,得△CBP,.
⑴ 求证:△PBP,是等腰直角三角形;
⑵ 猜想△PCP,的形状,并说明理由.
 (2)如果AB≠AC,∠BAC≠90°,点D在线段BC上运动.且∠BCA=45°时,如图丙请你判断线段CF、BD之间的位置关系,并说明理由(要求写出证明过程).
(2)如果AB≠AC,∠BAC≠90°,点D在线段BC上运动.且∠BCA=45°时,如图丙请你判断线段CF、BD之间的位置关系,并说明理由(要求写出证明过程).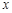 吨, 则粗加工的吨数为 吨,加工这批海产品需要 天, 可获利 元(用含
吨, 则粗加工的吨数为 吨,加工这批海产品需要 天, 可获利 元(用含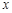 的代数式表示);
的代数式表示);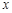 在什么范围内时, 该企业加工这批海产品的获利不低于120000元?
在什么范围内时, 该企业加工这批海产品的获利不低于120000元?湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com