如图，在水平地面点A处有一网球发射器向空中发射网球，网球飞行路线是一条抛物线，在地面上落点为B．有人在直线AB上点C（靠点B一侧）竖直向上摆放无盖的圆柱形桶，试图让网球落入桶内．已知AB＝4米，AC＝3米，网球飞行最大高度OM=5米，圆柱形桶的直径为0.5米，高为0.3米（网球的体积和圆柱形桶的厚度忽略不计）．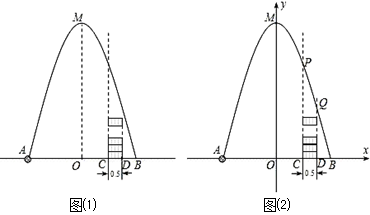

⑴ 在如图⑵建立的坐标系下，求网球飞行路线的抛物线解析式.
⑵ 若竖直摆放5个圆柱形桶时，则网球能落入桶内吗？说明理由；
⑶若要使网球能落入桶内，求竖直摆放的圆柱形桶的个数.

为了测量学校一棵参天古树的高度，我校数学兴趣小组做了如下探索：

实践1：利用一根标竿和一根皮尺设计出如图1的测量方案，把长为2.5米的标竿竖直插入离树（AB）8.7米的点E处，然后沿着直线BE后退到点D，这时眼睛恰好通过标竿顶点F，看到树的顶点A。再用皮尺测得DE＝2.7米。观察者目高CD＝1.6米。他们利用相似原理求得树高为5.4米。

实践2：提供选用的测量工具有①皮尺一根、②教学用三角板一副、③镜子一面、④测角仪一个。请你设计测量方案，并根据你所设计的测量方案回答下列问题。

（1） 在你设计的方案中，选用的测量工具是（用工具的序号填写）        。

（2） 在图2中画出你测量方案的示意图。

（3） 你需要测得示意图中哪些数据。并分别用a、b、c等表示测得数据      。

（4） 写出求树高（AB）的等式，AB＝             。（用a、b、c等字母表示）

如图，在水平地面点A处有一网球发射器向空中发射网球，网球飞行路线是一条抛物线，在地面上落点为B．有人在直线AB上点C（靠点B一侧）竖直向上摆放无盖的圆柱形桶，试图让网球落入桶内．已知AB＝4米，AC＝3米，网球飞行最大高度OM=5米，圆柱形桶的直径为0.5米，高为0.3米（网球的体积和圆柱形桶的厚度忽略不计）．

⑴ 在如图⑵建立的坐标系下，求网球飞行路线的抛物线解析式.

⑵ 若竖直摆放5个圆柱形桶时，则网球能落入桶内吗？说明理由；
⑶若要使网球能落入桶内，求竖直摆放的圆柱形桶的个数.

为了测量学校一棵参天古树的高度，我校数学兴趣小组做了如下探索：
实践1：利用一根标竿和一根皮尺设计出如图1的测量方案，把长为2.5米的标竿竖直插入离树（AB）8.7米的点E处，然后沿着直线BE后退到点D，这时眼睛恰好通过标竿顶点F，看到树的顶点A。再用皮尺测得DE＝2.7米。观察者目高CD＝1.6米。他们利用相似原理求得树高为5.4米。
实践2：提供选用的测量工具有①皮尺一根、②教学用三角板一副、③镜子一面、④测角仪一个。请你设计测量方案，并根据你所设计的测量方案回答下列问题。

（1）在你设计的方案中，选用的测量工具是（用工具的序号填写）        。
（2）在图2中画出你测量方案的示意图。
（3）你需要测得示意图中哪些数据。并分别用a、b、c等表示测得数据     。
（4）写出求树高（AB）的等式，AB＝             。（用a、b、c等字母表示）