
题目列表(包括答案和解析)
 23、观察探索题:
23、观察探索题:| 3 |
| 5 |
| 2 |
阅读材料并解答问题
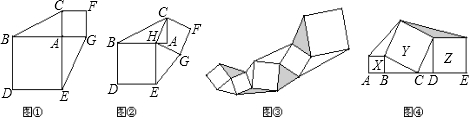
如图①,以Rt△ABC的直角边AB、AC为边分别向外作正方形ABDE和正方形ACFG,连结EG,可以得出结论△ABC的面积与△AEG的面积相等.
(1)在图①中的△ABC的直角边AB上任取一点H,连结CH,以BH、HC为边分别向外作正方形HBDE和正方形HCFG,连结EG,得到图②,则△HBC的面积与△HEG的面积的大小关系为 .
(2)如图③,若图形总面积是a,其中五个正方形的面积和是b,则图中阴影部分的面积是 .
(3)如图④,点A、B、C、D、E都在同一直线上,四边形X、Y、Z都是正方形,若图形总面积是m,正方形Y的面积是n,则图中阴影部分的面积是 .
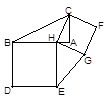
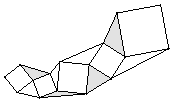
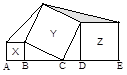
图① 图② 图③ 图④
阅读材料并解答问题
如图①,以Rt△ABC的直角边AB、AC为边分别向外作正方形ABDE和正方形ACFG,连结EG,可以得出结论△ABC的面积与△AEG的面积相等.
(1)在图①中的△ABC的直角边AB上任取一点H,连结CH,以BH、HC为边分别向外作正方形HBDE和正方形HCFG,连结EG,得到图②,则△HBC的面积与△HEG的面积的大小关系为 .
(2)如图③,若图形总面积是a,其中五个正方形的面积和是b,则图中阴影部分的面积是 .
(3)如图④,点A、B、C、D、E都在同一直线上,四边形X、Y、Z都是正方形,若图形总面积是m,正方形Y的面积是n,则图中阴影部分的面积是 .

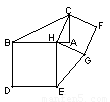


图① 图② 图③ 图④
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com