
题目列表(包括答案和解析)
(本题12分) 探究与发现:
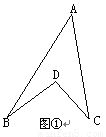
如图①所示的图形,像我们常见的学习用品——圆规.我们不妨把这样图形叫做“规形图”,那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥你的聪明才智,解决以下问题:
(一)观察“规形图”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;
(二)请你直接利用以上结论,解决以下三个问题:
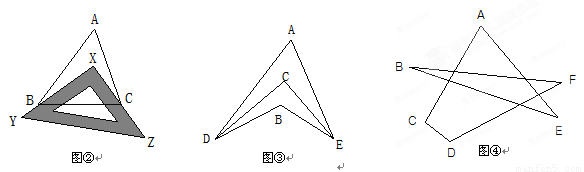
(1)如图②,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,若∠A=52°,则∠ABX+∠ACX =__________°;
(2)如图③,DC平分∠ADB,EC平分∠AEB,若∠DAE=50°,∠DBE=130°,求∠DCE的度数;
(3)如图④,求∠A+∠B+∠C+∠D+∠E+∠F的度数.
(本题12分)探究与发现:
如图①所示的图形,像我们常见的学习用品——圆规.我们不妨把这样图形叫做“规形图”,那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥你的聪明才智,解决以下问题:
(一)观察“规形图”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;
(二)请你直接利用以上结论,解决以下三个问题:
(1)如图②,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,若∠A=52°,则∠ABX+∠ACX =__________°;
(2)如图③,DC平分∠ADB,EC平分∠AEB,若∠DAE=50°,∠DBE=130°,求∠DCE的度数;
(3)如图④,求∠A+∠B+∠C+∠D+∠E+∠F的度数.
(本题12分) 探究与发现:
如图①所示的图形,像我们常见的学习用品——圆规.我们不妨把这样图形叫做“规形图”,那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥你的聪明才智,解决以下问题:
(一)观察“规形图”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;
(二)请你直接利用以上结论,解决以下三个问题:
(1)如图②,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,若∠A=52°,则∠ABX+∠ACX =__________°;
(2)如图③,DC平分∠ADB,EC平分∠AEB,若∠DAE=50°,∠DBE=130°,求∠DCE的度数;
(3)如图④,求∠A+∠B+∠C+∠D+∠E+∠F的度数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com