
题目列表(包括答案和解析)
数学课上,李老师出示了如下框中的题目.小敏与同桌小聪讨论后,进行了如下解答:
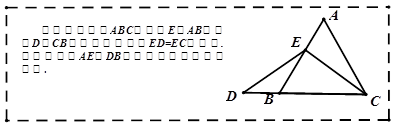
1.特殊情况,探索结论. 当点 为
为![]() 的中点时,确定线段
的中点时,确定线段![]() 与
与![]() 的大小关系,请你直接写出结论:
的大小关系,请你直接写出结论:![]()
![]() (填“>”,“<”或“=”).
(填“>”,“<”或“=”).
2.特例启发,解答题目
解:题目中,![]() 与
与![]() 的大小关系是:
的大小关系是:![]()
![]() (填“>”,“<”或“=”).理由如下:
(填“>”,“<”或“=”).理由如下:
如图1,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() .(请你完成以下解答过程)
.(请你完成以下解答过程)
3.拓展结论,设计新题
在等边三角形![]() 中,点
中,点![]() 在直线
在直线![]() 上,点
上,点![]() 在直线
在直线![]() 上,且
上,且![]() .若
.若![]() 的边长为1,
的边长为1,![]() ,则
,则![]() 的长为 (请你画出图形并直接写出结果,图没画或画错均不得分).
的长为 (请你画出图形并直接写出结果,图没画或画错均不得分).
(本题12分)数学课上,李老师出示了如下框中的题目.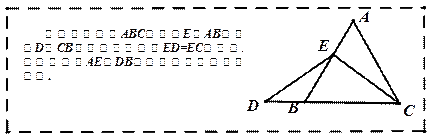
小敏与同桌小聪讨论后,进行了如下解答:
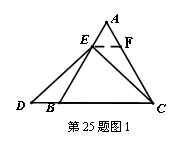
【小题1】(1)特殊情况,探索结论
当点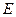 为
为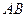 的中点时,如图1,确定线段
的中点时,如图1,确定线段 与
与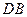 的大小关系,请你直接写出结论:
的大小关系,请你直接写出结论:
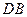 (填“>”,“<”或“=”).
(填“>”,“<”或“=”). 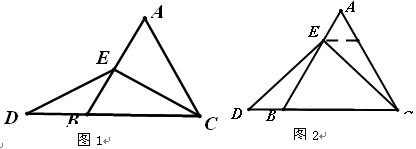
|
|
 与
与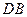 的大小关系是:
的大小关系是:
 (填“>”,“<”或“=”).理由如下:如图2,过点
(填“>”,“<”或“=”).理由如下:如图2,过点 作
作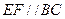 ,交
,交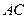 于点
于点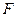 .
.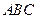 中,点
中,点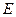 在直线
在直线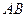 上,点
上,点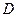 在直线
在直线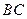 上,且
上,且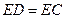 .若
.若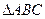 的边长为1,
的边长为1,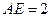 ,求
,求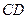 的长(请你直接写出结果).
的长(请你直接写出结果). 数学课上,李老师出示了如下框中的题目.小敏与同桌小聪讨论后,进行了如下解答:
【小题1】特殊情况,探索结论
当点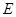 为
为 的中点时,如图1,确定线段
的中点时,如图1,确定线段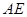 与
与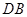 的大小关系,请你直接写出结论:
的大小关系,请你直接写出结论: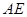
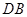 (填“>”,“<”或“=”).
(填“>”,“<”或“=”).
【小题2】特例启发,解答题目
解:题目中,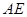 与
与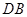 的大小关系是:
的大小关系是: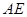
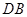 (填“>”,“<”或“=”).理由如下:如图2,过点
(填“>”,“<”或“=”).理由如下:如图2,过点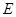 作
作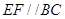 ,交
,交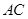 于点
于点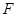 .
.
(请你完成以下解答过程)
【小题3】拓展结论,设计新题
在等边三角形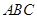 中,点
中,点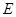 在直线
在直线 上,点
上,点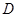 在直线
在直线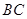 上,且
上,且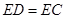 .若
.若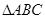 的边长为1,
的边长为1,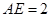 ,求
,求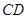 的长(请你直接写出结果).
的长(请你直接写出结果).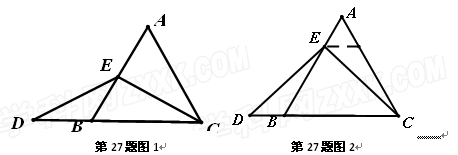
(本题12分)数学课上,李老师出示了如下框中的题目.
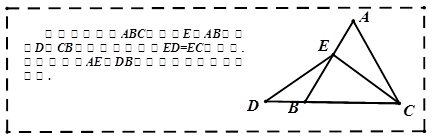
小敏与同桌小聪讨论后,进行了如下解答:
1.(1)特殊情况,探索结论
当点![]() 为
为![]() 的中点时,如图1,确定线段
的中点时,如图1,确定线段![]() 与
与![]() 的大小关系,请你直接写出结论:
的大小关系,请你直接写出结论:
![]()
 (填“>”,“<”或“=”).
(填“>”,“<”或“=”).

|
|
2.(2)特例启发,解答题目
解:题目中,![]() 与
与![]() 的大小关系是:
的大小关系是:![]()
![]() (填“>”,“<”或“=”).理由如下:如图2,过点
(填“>”,“<”或“=”).理由如下:如图2,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() .
.
(请你完成以下解答过程)
3.(3)拓展结论,设计新题
在等边三角形![]() 中,点
中,点![]() 在直线
在直线![]() 上,点
上,点![]() 在直线
在直线![]() 上,且
上,且![]() .若
.若![]() 的边长为1,
的边长为1,![]() ,求
,求![]() 的长(请你直接写出结果).
的长(请你直接写出结果).
(12分)阅读材料,解答下列问题.
例:当 时,如
时,如 则
则 ,故此时
,故此时 的绝对值是它本身
的绝对值是它本身
当 时,
时, ,故此时
,故此时 的绝对值是零
的绝对值是零
当 时,如
时,如 则
则 ,故此时
,故此时 的绝对值是它的相反数
的绝对值是它的相反数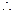 综合起来一个数的绝对值要分三种情况,即
综合起来一个数的绝对值要分三种情况,即
问:(1)这种分析方法涌透了 数学思想.
(2)请仿照例中的分类讨论的方法,分析二次根式 的各种展开的情况.
的各种展开的情况. (3)猜想
(3)猜想 与
与 的大小关系.
的大小关系.
(4)尝试用从以上探究中得到的结论来解决下面的问题: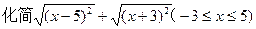
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com