（本题满分10分）

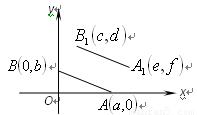
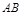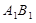（一）探究：如图，A，B的坐标为（2，0），（0，1）若将线段平移至，则=     ，=      。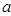

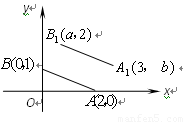
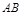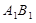（二）归纳：A，B的坐标为（a，0），（0，b）若将线段平移至，则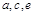三者关系为        ，

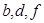三者间关系为       。

（三）应用：如图，抛物线y＝ax²＋bx＋c对称轴为直线x=1,交x轴于A、B两点,且点B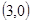，交y轴于C点。

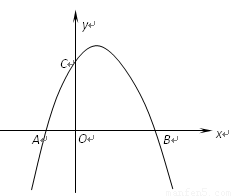
⑴求抛物线的函数关系式；

⑵将△AOC沿x轴翻折得到△AOC′，问：是否存在这样的点P，以P为旋转中心，将△AOC′ 旋转180°，使得A、C′的对称点E、G恰好在抛物线上？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由．

(本题满分10分)
已知：等腰三角形OAB在直角坐标系中的位置如图，点A的坐标为（），点B的坐标为（－6，0）.

（1）若△OAB关于y轴的轴对称图形是三角形O，请直接写出A、B的对称点的坐标；
（2）若将△沿x轴向右平移a个单位，此时点A恰好落在反比例函数的图像上，求a的值．

（11·贺州）（本题满分7分）

某校教学楼后面紧邻着一个山坡，坡上面是一块平地，如图所示，BC∥AD，BE⊥AD，斜坡AB长为26米，坡角∠BAD＝68°．为了减缓坡面防止山体滑坡，保障安全，学校决定对该斜坡进行改造，经地质人员勘测，当坡角不超过50°时，可确保山体不滑坡．

（1）求改造前坡顶到地面的距离BE的长（精确到0.1米）；

（2）如果改造时保持坡脚A不动，坡顶B沿BC向左移11米到F点处，问这样改造能确

保安全吗？

（参考数据：sin 68°≈0.93，cos 68°≈0.37，tan 68°≈2.48，sin 58°12’≈0.85，tan 49°30’

≈1.17）

.（本题满分5分）如图一根木棒放在数轴上，木棒的左端与数轴上的点A重合，右端与点B重合．

1.若将木棒沿数轴向右水平移动，则当它的左端移动到B点时，它的右端在数轴上所对应的数为20；若将木棒沿数轴向左水平移动，则当它的右端移动到A点时，则它的左端在数轴上所对应的数为5（单位：cm），由此可得到木棒长为　　 　cm．

2.由题(1)的启发,请你借助“数轴”这个工具帮助小红解决下列问题:

问题:一天，小红去问曾当过数学老师现在退休在家的爷爷的年龄，爷爷说：“我若是你现在这么大，你还要40年才出生；你若是我现在这么大，我已经125岁，是老寿星了，哈哈！”，请求出爷爷现在多少岁了？