新星电子科技公司积极应对2008年世界金融危机，及时调整投资方向，瞄准光伏产业，建成了太阳能光伏电池生产线．由于新产品开发初期成本高，且市场占有率不高等因素的影响，产品投产上市一年来，公司经历了由初期的亏损到后来逐步盈利的过程(公司对经营的盈亏情况每月最后一天结算1次)．公司累积获得的利润y(万元)与销售时间第x(月)之间的函数关系式(即前x个月的利润总和y与x之间的关系)对应的点都在如图所示的图象上．该图象从左至右，依次是线段OA、曲线AB和曲线BC，其中曲线AB为抛物线的一部分，点A为该抛物线的顶点，曲线BC为另一抛物线y＝－5x²＋205x－1230的一部分，且点A，B，C的横坐标分别为4，10，12

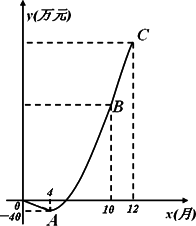
(1)求该公司累积获得的利润y(万元)与时间第x(月)之间的函数关系式；

(2)直接写出第x个月所获得S(万元)与时间x(月)之间的函数关系式(不需要写出计算过程)；

(3)前12个月中，第几个月该公司所获得的利润最多？最多利润是多少万元？

如图，二次函数y＝－ax²＋ax＋a(a＞0)的图象与y轴交于点A，与x轴交于点B、C，过A点作x轴的平行线交抛物线于另一点D，线段OC上有一动点P，连结DP，作PE⊥DP，交y轴于点E．

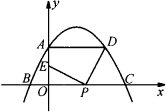
(1)当a变化时，线段AD的长是否变化？若变化，请说明理由；若不变，请求出AD的长．

(2)若a为定值，设OP＝x，OE＝y，试求y关于x的函数关系式．

(3)若在线段OC上存在不同的两点P₁、P₂使相应的点E₁、E₂都与点A重合，试求a的取值范围．

如图，在平面直角坐标系xOy中，我把由两条射线AE，BF和以AB为直径的半圆所组成的图形叫作图形C(注：不含AB线段)．已知A(－1，0)，B(1，0)，AE∥BF，且半圆与y轴的交点D在射线AE的反向延长线上．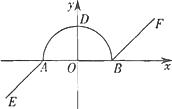

(1)求两条射线AE，BF所在直线的距离；

(2)当一次函数y＝x＋b的图象与图形C恰好只有一个公共点时，写出b的取值范围；当一次函数y＝x＋b的图象与图形C恰好只有两个公共点时，写出b的取值范围；

(3)已知□AMPQ(四个顶点A，M，P，Q按顺时针方向排列)的各顶点都在图形C上，且不都在两条射线上，求点M的横坐标x的取值范围．

企业的污水处理有两种方式，一种是输送到污水厂进行集中处理，另一种是通过企业的自身设备进行处理．某企业去年每月的污水量均为12000吨，由于污水厂处于调试阶段，污水处理能力有限，该企业投资自建设备处理污水，两种处理方式同时进行．1至6月，该企业向污水厂输送的污水量y₁(吨)与月份x(1≤x≤6，且x取整数)之间满足的函数关系如下表：

7至12月，该企业自身处理的污水量y₂(吨)与月份x(7≤x≤12，且x取整数)之间满足二次函数关系式为y₂＝ax²＋c(a≠0)．其图象如图所示．1至6月，污水厂处理每吨污水的费用：z₁(元)与月份x之间满足函数关系式：z₁＝x，该企业自身处理每吨污水的费用：z₂(元)与月份x之间满足函数关系式：z₂＝x－x²；7至12月，污水厂处理每吨污水的费用均为2元，该企业自身处理每吨污水的费用均为1.5元．

(1)请观察题中的表格和图象，用所学过的一次函数、反比例函数或二次函数的有关知识，分别直接写出y₁，y₂与x之间的函数关系式；

(2)请你求出该企业去年哪个月用于污水处理的费用W(元)最多，并求出这个最多费用；

(3)今年以来，由于自建污水处理设备的全面运行，该企业决定扩大产能并将所有污水全部自身处理，估计扩大产能后今年每月的污水量都将在去年每月的基础上增加a％，同时每吨污水处理的费用将在去年12月份的基础上增加(a－30)％，为鼓励节能降耗，减轻企业负担，财政对企业处理污水的费用进行50％的补助．若该企业每月的污水处理费用为18000元，请计算出a的整数值．(参考数据：≈15.2，≈20.5，≈28.4)