
题目列表(包括答案和解析)
某居民小区有一朝向为正南方向的居民楼(如图),该居民楼的一楼是高6米的小区超市,超市以上是居民住房.在该楼的前面15米处要盖一栋高20米的新楼.当冬季正午的阳光与水平线的夹角为32°时.
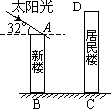
(1)问超市以上的居民住房采光是否有影响,为什么?(5分)
(2)若要使超市采光不受影响,两楼应相距多少米?(4分)
(结果保留整数,参考数据:![]() )
)
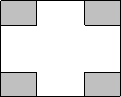 22、某小区有一长100m,宽80m的空地,现将其建成花园广场,设计图案如下,阴影区域为绿化区(四块绿化区是全等矩形),空白区域为活动区,且四周出口一样宽,宽度不小于50m,不大于60m.预计活动区每平方米造价60元,绿化区每平方米造价50元.设一块绿化区的长边为x m.
22、某小区有一长100m,宽80m的空地,现将其建成花园广场,设计图案如下,阴影区域为绿化区(四块绿化区是全等矩形),空白区域为活动区,且四周出口一样宽,宽度不小于50m,不大于60m.预计活动区每平方米造价60元,绿化区每平方米造价50元.设一块绿化区的长边为x m. 21、已知△ABC(如图),∠B=∠C=30度.请设计三种不同的分法,将△ABC分割成四个三角形,使得其中两个是全等三角形,而另外两个是相似但不全等的直角三角形.请画出分割线段,标出能够说明分法的所得三角形的顶点和内角度数(或记号),并在各种分法的空格线上填空.(画图工具不限,不要求证明,不要求写出画法)注:两种分法只要有一条分割线段位置不同,就认为是两种不同的分法.
21、已知△ABC(如图),∠B=∠C=30度.请设计三种不同的分法,将△ABC分割成四个三角形,使得其中两个是全等三角形,而另外两个是相似但不全等的直角三角形.请画出分割线段,标出能够说明分法的所得三角形的顶点和内角度数(或记号),并在各种分法的空格线上填空.(画图工具不限,不要求证明,不要求写出画法)注:两种分法只要有一条分割线段位置不同,就认为是两种不同的分法.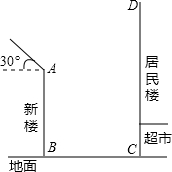 (2013•吴江市模拟)冬至是一年中太阳光照射最少的日子,如果此时楼房最低层能采到阳光,一年四季整座楼均能受到阳光照射,所以冬至是选房买房时确定阳光照射的最好时机.吴江某居民小区有一
(2013•吴江市模拟)冬至是一年中太阳光照射最少的日子,如果此时楼房最低层能采到阳光,一年四季整座楼均能受到阳光照射,所以冬至是选房买房时确定阳光照射的最好时机.吴江某居民小区有一| 2 |
| 3 |
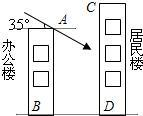 住房.在该楼的前面16米处要盖一栋高18米的办公楼.当冬季正午的阳光与水平线的夹角为35°时,问:
住房.在该楼的前面16米处要盖一栋高18米的办公楼.当冬季正午的阳光与水平线的夹角为35°时,问:湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com