
题目列表(包括答案和解析)
| |||||||||||
阅读并解答下列问题.
在给定的锐角△ABC中,求作一个正方形DEFG,使D,E落在BC边上,F,G分别落在AC,AB边上,作法如下.
第一步:画一个有三个顶点落在△ABC两边上的正方形![]() ;
;
第二步:连结![]() 并延长交AC于点F;
并延长交AC于点F;
第三步:过F点作FE⊥BC,垂足为点E;
第四步:过F点作FG∥BC交AB于点G;
第五步:过G点作GD⊥BC,垂足为点D.
四边形DEFG为所求作的正方形.如图所示.
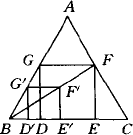
(1)证明上述所求作的四边形是正方形(EF=FG)
(2)在△ABC中,如果BC=6+![]() ,∠ABC=45°,∠BAC=75°,求上述正方形DEFG的边长.
,∠ABC=45°,∠BAC=75°,求上述正方形DEFG的边长.
如图,已知:⊙ 与⊙
与⊙ 相交于A,B两点,点
相交于A,B两点,点 在⊙
在⊙ 上,C为⊙
上,C为⊙ 中优弧上任意一点,直线CB交⊙
中优弧上任意一点,直线CB交⊙ 于D,连结
于D,连结 D.
D.
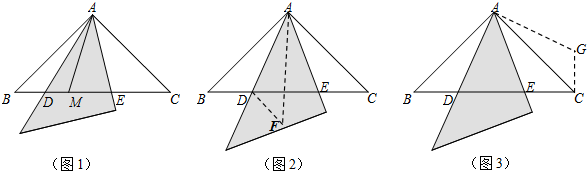
(1)用两种不同的方法,利用图(1)、图(2),证明:D ⊥AC.
⊥AC.
(2)若点C在劣弧 上,(1)中的结论是否仍然成立?请在图(3)中画出图形,并证明你的结论.
上,(1)中的结论是否仍然成立?请在图(3)中画出图形,并证明你的结论.

(1)如图1,在正方形ABCD中,O为正方形的中心,∠MON绕着O点自由的转动,角的两边与正方形的边BC、CD交于E、F.若∠MON=90°,正方形的面积等于S.求四边形OECF的面积.(用S表示)
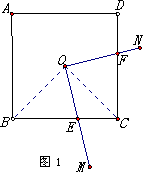
下面给出一种求解的思路,你可以按这一思路求解,也可以选择另外的方法去求.
解:连结OB、OC.∵O为正方形的中心,∴∠BOC=![]() =90°,∵∠MON=90°∴∠FOC+∠EOC=∠EOB+∠EOC=90°.∴∠FOC=∠EOB(下面请你完成余下的解题过程)
=90°,∵∠MON=90°∴∠FOC+∠EOC=∠EOB+∠EOC=90°.∴∠FOC=∠EOB(下面请你完成余下的解题过程)
(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),O是△ABC的中心,∠MON=120°,正三角形ABC的面积等于S.求四边形OECF的面积.(用S表示)
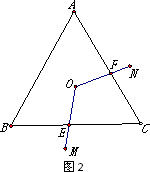
(3)若将(1)中的“正方形ABCD”改为“正n边形ABCD…X”,正n边形的面积等于S.请你作出猜想:当∠MON=________°时,四边形OECF的面积=________(用S表示,并直接写出答案,不需要证明)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com