
题目列表(包括答案和解析)
如图,菱形OABC的边长为4厘米,∠AOC=60°,动点P从O出发,以每秒1厘米的速度没O→A→B路线运动,点P出发2秒后,动点Q从O出发,在OA上以每秒1厘米的速度,在AB上以每秒2厘米的速度沿O→A→B路线运动,过P、Q两点分别作对角线AC的平行线.设P点运动的时间为X秒,这两条子行线在菱形上截出的图形(图中的阴影部分)的周长为y厘米.请你回答下列问题:
(1)当![]() 时,
时,![]() 的值是多少?
的值是多少?
(2)就下列各种情形,求![]() 与
与![]() 之间的函数关系式:
之间的函数关系式:
①![]() ②
②![]()
③![]() ④
④![]()
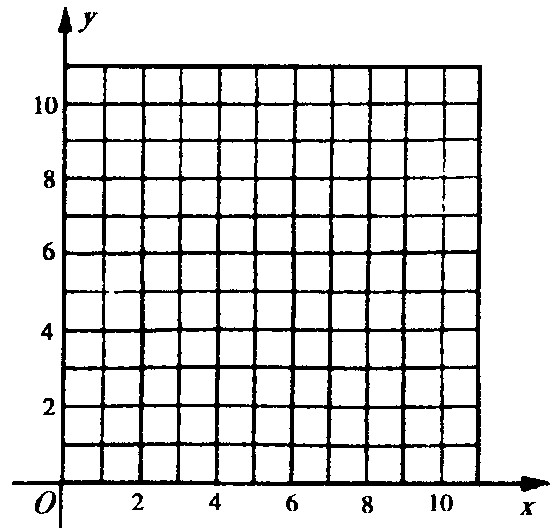
(3)在给出的直角坐标系中,用图象表示(2)中的各种情形下![]() 与
与![]() 的关系.
的关系.
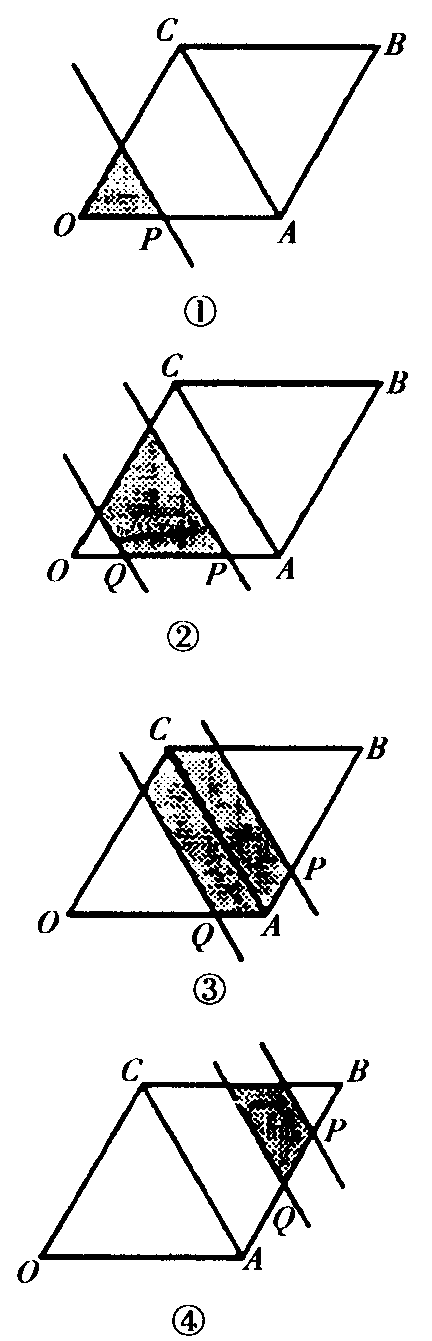
如图,菱形OABC的边长为4厘米,∠AOC=60°,动点P从O出发,以每秒1厘米的速度没O→A→B路线运动,点P出发2秒后,动点Q从O出发,在OA上以每秒1厘米的速度,在AB上以每秒2厘米的速度沿O→A→B路线运动,过P、Q两点分别作对角线AC的平行线.设P点运动的时间为X秒,这两条子行线在菱形上截出的图形(图中的阴影部分)的周长为y厘米.请你回答下列问题:
(1)当![]() 时,
时,![]() 的值是多少?
的值是多少?
(2)就下列各种情形,求![]() 与
与![]() 之间的函数关系式:
之间的函数关系式:
①![]() ②
②![]()
③![]() ④
④![]()
(3)在给出的直角坐标系中,用图象表示(2)中的各种情形下![]() 与
与![]() 的关系.
的关系.

某数学活动小组在作三角形的拓展图形,研究其性质时,经历了如下过程:
●操作发现:
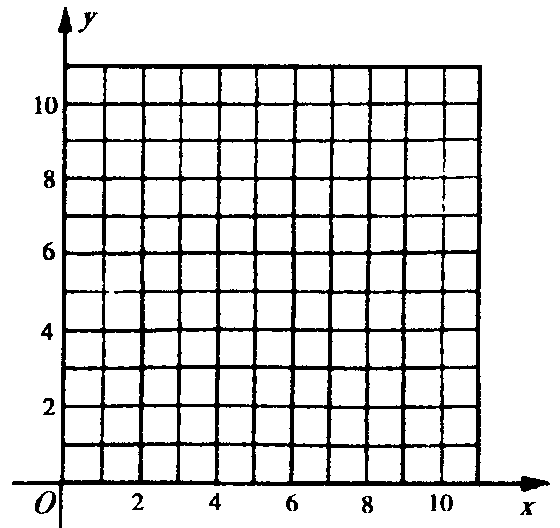
在等腰△ABC中,AB=AC,分别以AB和AC为斜边,向△ABC的外侧作等腰直角三角形,如图1所示,其中DF⊥AB于点F,EG⊥AC于点G,M是BC的中点,连接MD和ME,则下列结论正确的是 (填序号即可)
①AF=AG=![]() AB;②MD=ME;③整个图形是轴对称图形;④∠DAB=∠DMB.
AB;②MD=ME;③整个图形是轴对称图形;④∠DAB=∠DMB.
●数学思考:
在任意△ABC中,分别以AB和AC为斜边,向△ABC的外侧作等腰直角三角形,如图2所示,M是BC的中点,连接MD和ME,则MD和ME具有怎样的数量和位置关系?请给出证明过程;
●类比探索:
在任意△ABC中,仍分别以AB和AC为斜边,向△ABC的内侧作等腰直角三角形,如图3所示,M是BC的中点,连接MD和ME,试判断△MED的形状.
答: .

我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
(1
)写出你所学过的特殊四边形中是勾股四边形的两种图形的名称 , ;(2
)如图(1),已知格点(小正方形的顶点)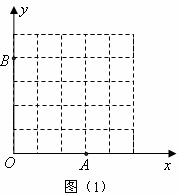
(3
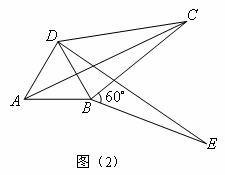
)如图(2),将求证:![]() ,即四边形
,即四边形![]() 是勾股四边形.
是勾股四边形.
阅读下列材料:
正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫格点三角形.
数学老师给小明同学出了一道题目:在图1正方形网格(每个小正方形边长为1)中画出格点△ABC,使![]() ,
,![]() ;
;
小明同学的做法是:由勾股定理,得![]() ,
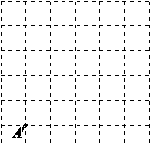
,![]() ,于是画出线段AB、AC、BC,从而画出格点△ABC.(1)请你参考小明同学的做法,在图2正方形网格(每个小正方形边长为1)中画出格点△
,于是画出线段AB、AC、BC,从而画出格点△ABC.(1)请你参考小明同学的做法,在图2正方形网格(每个小正方形边长为1)中画出格点△![]() (
(![]() 点位置如图所示),使
点位置如图所示),使![]() =
=![]() =5,
=5,![]() .(直接画出图形,不写过程);
.(直接画出图形,不写过程);
|
有怎样的数量关系,并证明你的猜想.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com