甲、乙两辆汽车同时分别从A、B两城沿同一条高速公路匀速驶向C城．已知A、C两城的距离为360km，B、C两城的距离为320km，甲车比乙车的速度快10km/h，结果两辆车同时到达C城．设乙车的速度为xkm/h．

（1）根据题意填写下表

（2）求甲、乙两车的速度．

【解析】（1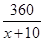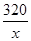），（2）甲的速度是90千米/时，乙的速度是80千米/时

【解析】（1）设乙的速度是x千米/时，那么甲的速度是（x+10）千米/时，根据时间=路程/速度

可求甲、乙两辆汽车所需时间；

（2）路程知道，且同时到达，可以时间做为等量关系列方程求解．

注意：为了使同学们更好地解答本题，我们提供了一种解题思路，你可以依照这个思路按下面的要求填空，并完成本题解答的全过程，也可以选用其他的解题方案，此时不必填空，只需按照解答题的一般要求，进行解答即可．
有一人患了流感，经过两轮传染后共有121人欢乐流感，每轮传染中平均一个人传染了几个人？
解题方案：
设每轮传染中平均一个人传染了x个人，
（Ⅰ）用含x的解析式表示：
第一轮后共有________人患了流感；
第二轮传染中，这些人中的每个人又传染了x个人，第二轮后共有________人患了流感；
（Ⅱ）根据题意，列出相应方程为________；
（Ⅲ）解这个方程，得________；
（Ⅳ）根据问题的实际意义，平均一个人传染了________个人．