如图，某飞机于空中探测某座山的高度，在点A处飞机的飞行高度是AF＝3700米，从飞机上观测山顶目标C的俯角是45°，飞机继续以相同的高度飞行300米到B处，此时观测目标C的俯角是50°，求这座山的高度CD．

（参考数据：sin50°≈0.77，cos50°≈0.64，tan50°≈1.20）．

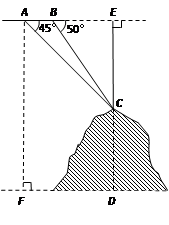
【解析】此题的关键是求出CE的长．可设CE为x千米，分别在Rt△ACE和Rt△BCE中，用x表示出AE、BE的长，根据AB=AE-BE=3即可求出CE的长；则CD=AF-EC，由此得解

如图1，点O为直线AB上一点，过点O作射线OC，使∠AOC=60°．将一把直角三角尺的直角顶点放在点O处，一边OM在射线OB上，另一边ON在直线AB的下方，其中∠OMN=30°。

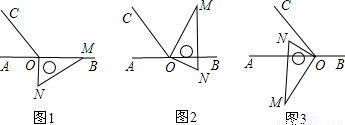
（1）将图1中的三角尺绕点O顺时针旋转至图2，使一边OM在∠BOC的内部，且恰好平分∠BOC，求∠CON的度数；

（2）将图1中的三角尺绕点O按每秒10°的速度沿顺时针方向旋转一周，在旋转的过程中，在第         秒时，边MN恰好与射线OC平行；在第         秒时，直线ON恰好平分锐角∠AOC。（直接写出结果）；

（3）将图1中的三角尺绕点O顺时针旋转至图3，使ON在∠AOC的内部，请探究∠AOM与∠NOC之间的数量关系，并说明理由．

【解析】此题考查了角的计算，关键是应该认真审题并仔细观察图形，找到各个量之间的关系，是解题的关键

如图1，点O为直线AB上一点，过点O作射线OC，使∠AOC=60°．将一把直角三角尺的直角顶点放在点O处，一边OM在射线OB上，另一边ON在直线AB的下方，其中∠OMN=30°。

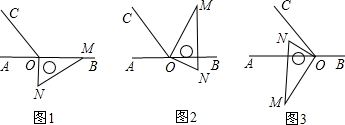
（1）将图1中的三角尺绕点O顺时针旋转至图2，使一边OM在∠BOC的内部，且恰好平分∠BOC，求∠CON的度数；

（2）将图1中的三角尺绕点O按每秒10°的速度沿顺时针方向旋转一周，在旋转的过程中，在第        秒时，边MN恰好与射线OC平行；在第        秒时，直线ON恰好平分锐角∠AOC。（直接写出结果）；

（3）将图1中的三角尺绕点O顺时针旋转至图3，使ON在∠AOC的内部，请探究∠AOM与∠NOC之间的数量关系，并说明理由．

【解析】此题考查了角的计算，关键是应该认真审题并仔细观察图形，找到各个量之间的关系，是解题的关键

如图，某飞机于空中探测某座山的高度，在点A处飞机的飞行高度是AF＝3700米，从飞机上观测山顶目标C的俯角是45°，飞机继续以相同的高度飞行300米到B处，此时观测目标C的俯角是50°，求这座山的高度CD．

（参考数据：sin50°≈0.77，cos50°≈0.64，tan50°≈1.20）．

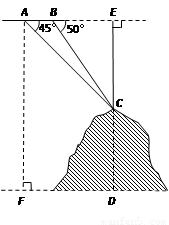
【解析】此题的关键是求出CE的长．可设CE为x千米，分别在Rt△ACE和Rt△BCE中，用x表示出AE、BE的长，根据AB=AE-BE=3即可求出CE的长；则CD=AF-EC，由此得解

甲、乙两同学学习计算机打字，甲打一篇3000字的文章与乙打一篇2400字的文章所用的时间相同．已知甲每分钟比乙每分钟多打12个字，问甲、乙两人每分钟各打多少个字？

李明同学是这样解答的：

设甲同学打印一篇3 000字的文章需要分钟，

根据题意，得                      （1）

解得：．

经检验是原方程的解．                          （2）

答：甲同学每分钟打字50个，乙同学每分钟打字38个．  （3）

（1）请从（1）、（2）、（3）三个步骤说明李明同学的解答过程是否正确，若有不正确的步骤请改正过来．

（2）请你用直接设未知数列方程的方法解决这个问题．

【解析】此题解题关键是找到等量关系：甲每分钟比乙每分钟多打12个字，然后根据等量关系列出方程。