如图，矩形ABCD中，E为BC上一点，DF⊥AE于F.(1)ΔABE与ΔADF相似吗？请说明理由.(2)若AB=6，AD=12，BE=8，求DF的长.

【解析】（1）根据矩形的性质和DF⊥AE，可得∠ABE=∠AFD=90°，∠AEB=∠DAF，即可证明△ABE∽△ADF．

（2）利用△ABE∽△ADF，得，再利用勾股定理，求出AE的长，然后将已知数值代入即可求出DF的长

如图，△ABC中，∠BAC=90°，AC=2，AB=，△ACD是等边三角形.

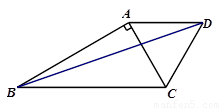
（1）求∠ABC的度数.

（2）以点A为中心，把△ABD顺时针旋转60°，

画出旋转后的图形.

（3）求BD的长度.

【解析】（1）利用正切的知识可得出答案．

（2）根据旋转角度、旋转中心、旋转方向找出各点的对称点，顺次连接即可；

（3）根据旋转的性质可得△ACE≌△ADB，从而确定∠EBC=90°，然后利用勾股定理即可解答

如图，在□ABCD中，对角线AC、BD相交于点O，点E在BD的延长线上，且△EAC是等边三角形，若AC=8，AB=5，求ED的长．

【解析】利用四边形ABCD是平行四边形，△EAC是等边三角形求得EO⊥AC.利用勾股定理求出BO,EO，即可求得ED的长

如图，在□ABCD中，对角线AC、BD相交于点O，点E在BD的延长线上，且△EAC是等边三角形，若AC=8，AB=5，求ED的长．

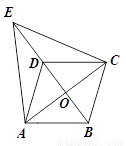
【解析】利用四边形ABCD是平行四边形，△EAC是等边三角形求得EO⊥AC.利用勾股定理求出BO,EO，即可求得ED的长

如图，在△ABC中，点D是BC上一点，∠B＝∠DAC＝45°．

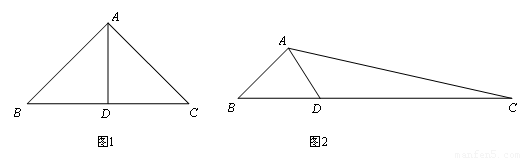
（1）如图1，当∠C＝45°时，请写出图中一对相等的线段；_________________

（2）如图2，若BD＝2，BA＝，求AD的长及△ACD的面积．

【解析】（1）由题意知△ABC、△ABD、△ACD为等腰直角三角形，可求得，（2）利用勾股定理求得AD的长，求得AED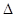CGD，即可求得△ACD的面积