
题目列表(包括答案和解析)
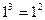
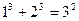
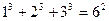

(本题6分)探索与思考:
观察下列等式: 
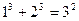
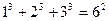
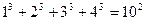
……………………
【小题1】(1)想一想:等式左边各项幂的底数与右边幂的底数有什么关系?
【小题2】(2)试一试:13 + 23 + 3 3 + 43 + … + 10 3 = ____________.
【小题3】(3)猜一猜:可得出什么规律(可用带字母的等式表示,也可用文字表述):
(本题6分)探索与思考:
观察下列等式: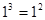
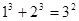
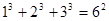
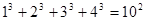
……
(1)想一想:等式左边各项幂的底数与右边幂的底数有什么关系?
(2)试一试:13 + 23 + 3 3 + 43 + … + 10 3 = ____________.
(3)猜一猜:可得出什么规律(可用带字母的等式表示,也可用文字表述)。
(本题6分)探索与思考:
观察下列等式:
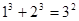
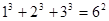

……
(1)想一想:等式左边各项幂的底数与右边幂的底数有什么关系?
(2)试一试:13 + 23 + 3 3 + 43 + … + 10 3 = ____________.
(3)猜一猜:可得出什么规律(可用带字母的等式表示,也可用文字表述)。
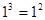
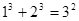
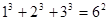
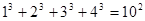
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com