（2012•达州）【问题背景】
若矩形的周长为1，则可求出该矩形面积的最大值．我们可以设矩形的一边长为x，面积为s，则s与x的函数关系式为：s=-x2+

1

2

x(x＞0），利用函数的图象或通过配方均可求得该函数的最大值．
【提出新问题】
若矩形的面积为1，则该矩形的周长有无最大值或最小值？若有，最大（小）值是多少？
【分析问题】
若设该矩形的一边长为x，周长为y，则y与x的函数关系式为：y=2(x+

1

x

)（x＞0），问题就转化为研究该函数的最大（小）值了．
【解决问题】
借鉴我们已有的研究函数的经验，探索函数y=2(x+

1

x

)（x＞0）的最大（小）值．
（1）实践操作：填写下表，并用描点法画出函数y=2(x+

1

x

)（x＞0）的图象：

x	…	1 4	1 3	1 2	1	2	3	4	…
y	…								…

（2）观察猜想：观察该函数的图象，猜想当x=时，函数y=2(x+

1

x

)（x＞0）有最值（填“大”或“小”），是．
（3）推理论证：问题背景中提到，通过配方可求二次函数s=-x2+

1

2

x(x＞0）的最大值，请你尝试通过配方求函数y=2(x+

1

x

)（x＞0）的最大（小）值，以证明你的猜想．〔提示：当x＞0时，x=(

x

)2〕

问题背景：
若矩形的周长为1，则可求出该矩形面积的最大值．我们可以设矩形的一边长为x，面积为s，则s与x的函数关系式为：s=-x2+

1

2

x（x＞0），利用函数的图象或通过配方均可求得该函数的最大值．
提出新问题：
若矩形的面积为1，则该矩形的周长有无最大值或最小值？若有，最大（小）值是多少？
分析问题：
若设该矩形的一边长为x，周长为y，则y与x的函数关系式为：y=2(x+

1

x

)（x＞0），问题就转化为研究该函数的最大（小）值了．
解决问题：
借鉴我们已有的研究函数的经验，探索函数y=2(x+

1

x

)（x＞0）的最大（小）值．
（1）实践操作：填写下表，并用描点法画出函数y=2(x+

1

x

)（x＞0）的图象：

x	…	1/4	1/3	1/2	1	2	3	4	…
y	…	17 2	20 3	5	4	5	20 3	17 2	…

（2）观察猜想：观察该函数的图象，猜想当x=时，函数y=2(x+

1

x

)（x＞0）有最值（填“大”或“小”），是．
（3）推理论证：问题背景中提到，通过配方可求二次函数s=-x2+

1

2

x（x＞0）的最大值，请你尝试通过配方求函数y=2(x+

1

x

)（x＞0）的最大（小）值，以证明你的猜想．〔提示：当x＞0时，x=(

x

)2〕

小涵、小敏和小灵三位同学，对小雅书包里的书的本数作出不同的估计：
小涵说：“书包里至少有10本书”
小敏说：“不！不！书包里的书不到10本”
小灵接着说：“书包里最少有1本书”
这时，小雅说：“你们三个人的话，只有1个人正确”
请问：小雅书包里有几本书？
这时一道逻辑推理题
根据题意，三人的估计有三种可能情形，依次是：①对、错、错；②错、对、错；③错、错、对．然后再一一分析之．
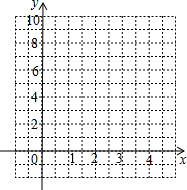
现在我们利用数轴知识，画成下图：

从图中可见：
（1）若书包里有1或2或…或9本书，则小敏与小灵的估计都对了，不合题意；
（2）若书包里至少有10本书，则小涵与小灵的伏击都对了，也不合题意；
（3）若书包里有0本书（即书包里没有书），只有小敏的估计正确，符合题意．
由此实例可见，利用数轴知识来解，真是一目了然，比平时的逻辑推理方法，更容易理解．
仿此，请大家做下面的一道趣题：
甲、乙、丙、丁思维同学对小雅同学书包里的数作出估计：
甲说：“书包里之多12本书”
乙说：“不！不！书包里的书至少有5本，至多11本”
丙说：“书包里至多8本书”
丁说：“我估计乙、丙两人中至少有一人估计对了”
小雅说：“你们4个人的话，只有1个人正确”
则甲、乙、丙、丁中估计正确，小雅书包里有书．