
题目列表(包括答案和解析)
 25、如图,△AOC≌△BOD,试证明AC∥BD.
25、如图,△AOC≌△BOD,试证明AC∥BD.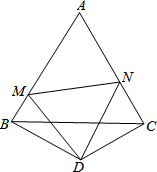 D为等边△ABC外一点,且BD=CD,∠BDC=120°,点M,N分别在AB,AC上,若BM+CN=MN
D为等边△ABC外一点,且BD=CD,∠BDC=120°,点M,N分别在AB,AC上,若BM+CN=MN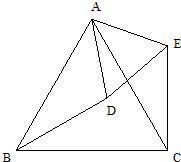 22、如图:△ABC和△ADE是等边三角形.证明:BD=CE.
22、如图:△ABC和△ADE是等边三角形.证明:BD=CE. 填空:已知,(如图)在△ABC中,BD为∠ABC的平分线,AB=BC,点P在BF上,PM⊥AD于M,
填空:已知,(如图)在△ABC中,BD为∠ABC的平分线,AB=BC,点P在BF上,PM⊥AD于M, (2012•沐川县二模)本题为选做题,从甲乙两题中选做一题即可,如果两题都做,只以甲题计分.
(2012•沐川县二模)本题为选做题,从甲乙两题中选做一题即可,如果两题都做,只以甲题计分.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com