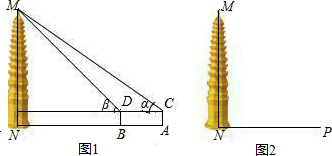
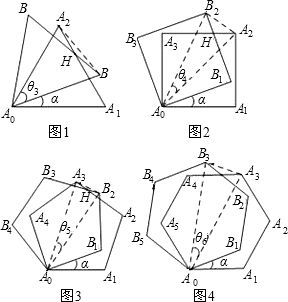
课题:两个重叠的正多形,其中的一个绕某一顶点旋转所形成的有关问题.
实验与论证:
设旋转角∠A
1A
0B
1=α(α<∠A
1A
0A
2),θ
3、θ
4、θ
5、θ
6所表示的角如图所示.
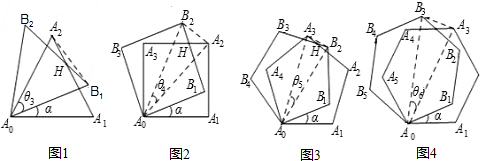
(1)用含α的式子表示解的度数:θ
3=
,θ
4=
,θ
5=
;
(2)图1-图4中,连接A
0H时,在不添加其他辅助线的情况下,是否存在与直线A
0H垂直且被它平分的线段?若存在,请选择其中的一个图给出证明;若不存在,请说明理由;
归纳与猜想:
设正n边形A
0A
1A
2…A
n-1与正n边形A
0B
1B
2…B
n-1重合(其中,A
1与B
1重合),现将正边形A
0B
1B
2…B
n-1绕顶点A
0逆时针旋转α(0°<α<
°);
(3)设θ
n与上述“θ
3、θ
4、…”的意义一样,请直接写出θ
n的度数;
(4)试猜想在正n边形的情形下,是否存在与直线A
0H垂直且被它平分的线段?若存在,请将这条线段用相应的顶点字母表示出来(不要求证明);若不存在,请说明理由.