
阅读理解
九年级一班数学学习兴趣小组在解决下列问题中,发现该类问题不仅可以应用“三角形相似”知识解决问题,还可以“建立直角坐标系、应用一次函数”解决问题.
请先阅读下列“建立直角坐标系、应用一次函数”解决问题的方法,然后再应用此方法解决后续问题.
问题:如图(1),直立在点D处的标杆CD长3m,站立在点F处的观察者从点E处看到标杆顶C、旗杆顶A在一条直线上.已知BD=15m,FD=2m,EF=1.6m,求旗杆高AB.
解:建立如图(2)所示的直角坐标系,则线段AE可看作一个一次函数的图象.
由题意可得各点坐标为:点E(0,1.6),C(2,3),B(17,0),且所求的高度就为点A的纵坐标.
设直线AE的函数关系式为y=kx+b.
把E(0,1.6),C(2,3)代入得
解得

∴y=0.7x+1.6.
∴当x=17时,y=0.7×17+1.6=13.5,即AB=13.5(m).
解决问题
请应用上述方法解决下列问题:
如图(3),河对岸有一路灯杆AB,在灯光下,小明在点D处测得自己的影长DF=3m,BD=9m,沿BD方向到达点F处再测得自己的影长FG=4m.如果小明的身高为1.6m,求路灯杆AB的高度.

 阅读理解
阅读理解
 解得
解得


 阅读理解
阅读理解 解得
解得

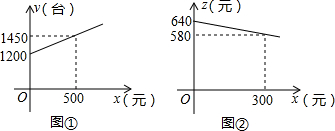 多少元?并求出总收益w的最大值.
多少元?并求出总收益w的最大值.