
题目列表(包括答案和解析)
 12、如图,点P是∠AOB的角平分线OC上一点,分别连接 AP、BP,若再添加一个条件即可判定△APO≌△BPO,则在以下条件中:①∠A=∠B;②∠APO=∠BPO;③∠APC=∠BPC;④AP=BP;⑤OA=OB,不一定正确的是
12、如图,点P是∠AOB的角平分线OC上一点,分别连接 AP、BP,若再添加一个条件即可判定△APO≌△BPO,则在以下条件中:①∠A=∠B;②∠APO=∠BPO;③∠APC=∠BPC;④AP=BP;⑤OA=OB,不一定正确的是
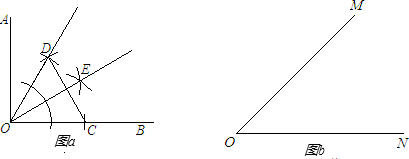
| 1 |
| x |
| 1 |
| 3 |
| 1 |
| a |
| 1 |
| b |
| 1 |
| 3 |
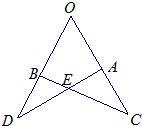 15、如图,已知,在△OAD和△OBC中,OD=OC,若不增加任何字母与辅助线,要使△OAD≌△OBC.则还需增加一个条件是
15、如图,已知,在△OAD和△OBC中,OD=OC,若不增加任何字母与辅助线,要使△OAD≌△OBC.则还需增加一个条件是 13、如图,OA=OC,则需补充条件
13、如图,OA=OC,则需补充条件| BP |
| PO |
| 1 |
| 3 |
| CP |
| PA |
| 1 |
| 3 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com