(1)已知2x－3y=6，则y关于x的函数关系式为______________，x关于y的函数关系式为______________．

(2)一个弹簧不挂物体时长10cm，挂上物体后，每挂1kg物体，弹簧就伸长1.5cm．

①如果所挂物体的总质量是x(kg)，那么弹簧伸长的长度y(cm)可表示为___________，在这个问题中，自变量是__________，函数是____________．

②如果所挂物体的总质量为x(kg)，那么弹簧的总长度y(cm)关于x的函数关系式为______________．这其中_________是自变量，_________是函数．

(3)列函数关系式．

①球的体积V表示半径R的函数关系式为___________．

②圆的面积S是圆的周长C的函数关系式为___________．

③已知等腰三角形的周长为18，则腰长a关于底边长b的解析式为___________，在这个问题中自变量的取值范围是___________．

④等腰三角形的顶角a (度)与底角b (度)之间的函数关系为___________，自变量的取值范围___________．

⑤等腰三角形的底角β(度)与顶角a (度)的关系为___________，自变量的取值范围是___________．列函数关系式时，要分清谁是函数及要求的意义．

(1)已知2x－3y=6，则y关于x的函数关系式为______________，x关于y的函数关系式为______________．

(2)一个弹簧不挂物体时长10cm，挂上物体后，每挂1kg物体，弹簧就伸长1.5cm．

①如果所挂物体的总质量是x(kg)，那么弹簧伸长的长度y(cm)可表示为___________，在这个问题中，自变量是__________，函数是____________．

②如果所挂物体的总质量为x(kg)，那么弹簧的总长度y(cm)关于x的函数关系式为______________．这其中_________是自变量，_________是函数．

(3)列函数关系式．

①球的体积V表示半径R的函数关系式为___________．

②圆的面积S是圆的周长C的函数关系式为___________．

③已知等腰三角形的周长为18，则腰长a关于底边长b的解析式为___________，在这个问题中自变量的取值范围是___________．

④等腰三角形的顶角a (度)与底角b (度)之间的函数关系为___________，自变量的取值范围___________．

⑤等腰三角形的底角β(度)与顶角a (度)的关系为___________，自变量的取值范围是___________．列函数关系式时，要分清谁是函数及要求的意义．

已知：四边形ABCD为圆内接矩形，过点D作圆的切线DP，交BA的延长线于点P，且PD=15，PA=9．
（1）求AD与AB的长；
（2）如果点E为PD的一个动点（不与运动至P，D），过点E作直线EF，交PB于点F，并将四边形PBCD的周长平分，记△PEF的面积为y，PE的长为x，请求出y关于x的函数关系式；
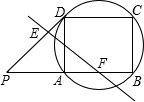（3）如果点E为折线DCB上一个动点（不与运动至D，B），过点E作直线EF交PB于点F，试猜想直线EF能否将四边形PBCD的周长和面积同时平分？若能，请求出BF的长．若不能，请说明理由．

数学家们通过长期的研究，得到了关于“等周问题”的重要结论：在周长相同的所有封闭平面曲线中，以圆所围成的面积最大．
“等周问题”虽然较为繁杂，但其根本思想基于下面2个事实：
事实1：等周长n边形的面积，当图形为正n边形时，其面积最大；
事实2：等周长n边形的面积，当边数n越大时，其面积也越大．
为了理解这些事实的合理性，曙光数学小组走出校门展开了下列课题研究．请你帮助他们解决其中的一些问题．
现有长度为100m的篱笆（可弯曲围成一个区域）．
（1）如果用篱笆围成一个长方形鸡场，怎样围才能使鸡场的面积最大？为什么？
（2）如果用篱笆围成一个正五边形鸡场，那么与（1）中的正方形鸡场比较，哪个面积更大？请在事实1的基础上证明事实2：“等周长n边形的面积，当边数n越大时，其面积也越大．”
（3）利用事实1和事实2，请对“等周问题”的重要结论作出较为合理的解释．
（4）爱动脑筋的小明提出一个问题：如果借用一条充分长的直墙，将篱笆围成一个四边形鸡场，为了使鸡场的面积尽量大，所围成的长方形鸡场的长是宽的2倍（如图）．你觉得他讲的是否有道理？你有没有更好的方法，使围成的四边形鸡场的面积更大？如果有，请说明你的方法．