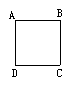
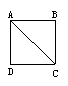
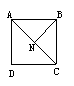
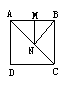
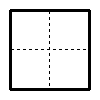
将一张正方形纸按图所示的方式二次折叠,折叠后再按图所示沿MN裁剪,则可得(   ).

    A.多个等腰直角三角形；  B.一个等腰直角三角形和一个正方形；

C.四个相同的正方形；    D.两个相同的正方形。

将一张正方形纸片剪成四个大小、形状一样的小正方形（如右下图所示），记为第一次操作，然后将其中的一片又按同样的方法剪成四小片，记为第二次操作，如此循环进行下去．请将下表中空缺的数据填写完整，并解答所提出的问题：

操作次数	1	2	3	4	…
正方形个数	4	7			…

⑴如果剪100次，共能得到__________个正方形．

⑵如果剪n次共能得到b_n个正方形，试用含有n、b_n的等式表示它们之间的数量关系．

   _________________________________________

⑶若原正方形的边长为1，设表示第n次所剪的正方形的边长，试用含n的式子表示．

__________________________________________．

⑷试猜想与原正方形边长的数量关系，并用等式写出这个关系．

__________________________________________．

如图，正方形表示一张纸片，根据要求，需通过多次分割，将正方形纸片分割成若干个直角三角形，操作过程如下：第一次分割，将正方形纸片分成4个全等的直角三角形；第二次分割，将上次得到的直角三角形中的一个再分成4个全等直角三角形；以后按第二次分割的做法进行下去．

(1)请你设计出两种符合题意的分割方案图(要求在图1、图2中分别画出每种方案的第一次和第二次的分割线，只要有一条分割线段不同，就视为一种不同方案，图3供操作、实验用)．

(2)设正方形的边长为a，请你就其中一种方案通过操作和观察将第二、第三次分割后所得的最小直角三角形的面积S填入下表：

(3)在条件(2)下，请你猜想：分割所得的最小直角三角形的面积S与分割次数n有什么关系？用数学表达式表示出来．

　如图6所示，正方形ABCD的边长为12，划分成12×12个小正方形格，将边长为n（n为整数，且2≤n≤11）的黑白两色正方形纸片按图中的方式，黑白相间地摆放，第一张n×n的纸片正好盖住正方形ABCD左上角的n×n个小正方形格，第二张纸片盖住第一张纸片的部分恰好为(n－1)×(n－1)个小正方形.如此摆放下去，直到纸片盖住正方形ABCD的右下角为止.

请你认真观察思考后回答下列问题：

（1）由于正方形纸片边长n的取值不同，完成摆放时所使用正方形纸片的张数也不同，请填写下表：

纸片的边长n	2	3	4	5	6
使用的纸片张数

（2）设正方形ABCD被纸片盖住的面积（重合部分只计一次）为S₁，未被盖住的面积为S₂.

①当n＝2时，求S₁∶S₂的值；

②是否存在使得S₁＝S₂的n值？若存在，请求出来；若不存在，请说明理由.