练习册

  • 练习册
  • 试题
    猜想数量关系 例4如图5.在梯形ABCD中.AB∥CD...E为AD边上的任意一点.EF∥AB.且EF交BC于点F.某学生在研究这一问题时.发现如下事实: ①当时.有, ②当时.有, ③当时.有． 当时.参照上述研究结论.请你猜想用k表示DE的一般结论.并给出证明, (2)现有一块直角梯形田地.其中AB∥CD..310米.170米.70米．若要将这块地分割成两块.由两农户来承包.要求这两块地均为直角梯形.且它们的面积相等．请你给出具体分割方案． 【查看更多】

     

    题目列表(包括答案和解析)

    【图形变换的探究与猜想】
    从特殊到一般，从全等到相似；求证线段的数量关系或位置关系．关键是第一问的全等的证明，发现全等的三角形，一般是利用ASA完成证明，从而得到需要证明的相似三角形（利用两边对应成比例且夹角相等）．
    例：正方形ABCD，E为直线AB上任意一点，DF⊥DE交直线BC于点F，直线EF、AC交于点H，连接DH．

    （1）①如图1，当点E在边AB上时，判断线段DH与线段EF之间的数量关系和位置关系；
    ②如图2，当点E在边AB的反向延长线上时，判断线段DH与线段EF之间的数量关系和位置关系；写出你的结论并从①、②中任选一个证明；
    （2）如图3，若点E在AB边的延长线上，其它条件不变，完成图3，判断线段DH与线段EF之间的数量关系和位置关系，直接写出你的结论，不需要证明；
    （3）如图4，若将图1中的正方形ABCD改为矩形ABCD为正方形，且AB=kAD，其它条件不变，判断线段DH与线段EF之间的数量关系和位置关系，直接写出结论，不需要证明．

    查看答案和解析>>

    三角板是我们数学学习必不可少的工具，如图1是一副含45°和30°的三角板，其中三角板ABC中，∠A=∠B=45°，AC=BC；三角板DEF中，∠D=60°，∠E=30°．
    现在我们进行如下操作：把含30°的三角板的直角顶点F位于另一三角板的斜边中点上，边FD与AC相交于点M，边FE与BC相交于点N，将三角板DEF绕点F旋转，点M、N分别在线段AC、BC上相应移动．
    （1）请你探究：当∠AFD=45°时（如图2），FM与FN有怎样的数量关系？请说明理由；
    （2）请你猜想：在三角板DEF绕点F旋转过程中，（1）中FM 与FN的数量关系还成立吗？如果成立，请说明理由；如果不成立，请举反例说明（图3供实验、操作备用）．
    精英家教网精英家教网

    查看答案和解析>>

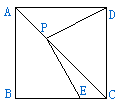
    已知四边形ABCD，点E是BC边上的一个动点（点E不与B、C两点重合），线段BE的垂直平分线交对角线AC于点P，联结DP，PE.

    （1）如图（1），若四边形ABCD是正方形，猜想PD与PE的数量关系，并证明你的结论；

    （2）若四边形ABCD是矩形，（1）中的结论还成立吗？如果成立，证明你的结论；如果不成立，用尺规作图的方法举反例证明（保留作图痕迹，不写作法）；

    （3）若四边形ABCD是矩形，AB＝6，cos∠ACD＝ ，设AP＝x，△PCE的面积为y，求y与x之间的函数关系式.    

     

    查看答案和解析>>


    同步练习册答案