已知数列{}中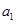，=1，前n项和。

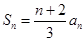    （Ⅰ）求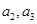

    (Ⅱ)求{}的通项公式。

【解析】本试题主要考查了数列的通项公式与数列求和的相结合的综合运用。

【点评】试题出题比较直接，没有什么隐含的条件，只要充分利用通项公式和前n项和的关系式变形就可以得到结论。

 

杨辉是中国南宋末年的一位杰出的数学家、数学教育家、杨辉三角是杨辉的一大重要研究成果，它的许多性质与组合数的性质有关，杨辉三角中蕴藏了许多优美的规律．如图是一个11阶杨辉三角：
（1）求第20行中从左到右的第4个数；
（2）若第n行中从左到右第14与第15个数的比为

2

3

，求n的值；
（3）求n阶（包括0阶）杨辉三角的所有数的和；
（4）在第3斜列中，前5个数依次为1，3，6，10，15；第4斜列中，第5个数为35．显然，1+3+6+10+15=35．事实上，一般地有这样的结论：第m斜列中（从右上到左下）前k个数之和，一定等于第m+1斜列中第k个数．试用含有m、k（m，k∈N×）的数学公式表示上述结论，并给予证明．

第0行												1	…	…	…	…	…	…	…	…	…	…	…	…	第1斜列
第1行											1		1	…	…	…	…	…	…	…	…	…	…	…	第2斜列
第2行										1		2		1	…	…	…	…	…	…	…	…	…	…	第3斜列
第3行									1		3		3		1	…	…	…	…	…	…	…	…	…	第4斜列
第4行								1		4		6		4		1	…	…	…	…	…	…	…	…	第5斜列
第5行							1		5		10		10		5		1	…	…	…	…	…	…	…	第6斜列
第6行						1		6		15		20		15		6		1	…	…	…	…	…	…	第7斜列
第7行					1		7		21		35		35		21		7		1	…	…	…	…	…	第8斜列
第8行				1		8		28		56		70		56		28		8		1	…	…	…	…	第9斜列
第9行			1		9		36		84		126		126		84		36		9		1	…	…	…	第10斜列
第10行		1		10		45		120		210		252		210		120		45		10		1	…	…	第11斜列
第11行	1		11		55		165		330		462		462		330		165		55		11		1	…	第12斜列
										11阶杨辉三角