
题目列表(包括答案和解析)
如果一个实数数列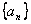 满足条件:
满足条件: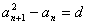 (
(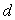 为常数,
为常数,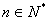 ),则称这一数列
“伪等差数列”,
),则称这一数列
“伪等差数列”, 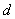 称为“伪公差”。给出下列关于某个伪等差数列
称为“伪公差”。给出下列关于某个伪等差数列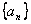 的结论:
的结论:
①对于任意的首项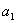 ,若
,若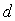 <0,则这一数列必为有穷数列;
<0,则这一数列必为有穷数列;
②当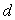 >0,
>0, 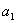 >0时,这一数列必为单调递增数列;
>0时,这一数列必为单调递增数列;
③这一数列可以是一个周期数列;
④若这一数列的首项为1,伪公差为3,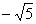 可以是这一数列中的一项;
可以是这一数列中的一项;
⑤若这一数列的首项为0,第三项为-1,则这一数列的伪公差可以是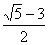 。
。
其中正确的结论是________________.
 ,其中aij表示第i行第j列的数.已知每一行中的数依次都成等差数列,每一列中的数依次都成等比数列,且公比均为q,a11=
,其中aij表示第i行第j列的数.已知每一行中的数依次都成等差数列,每一列中的数依次都成等比数列,且公比均为q,a11=| 1 |
| 2 |
| 1 |
| 4 |
| 36 |
| An |
| bn |
| an |
| c | 2 1 |
| c | 2 7 |
| 200 |
| an |
| lim |
| n→∞ |
| 1 |
| S1 |
| 1 |
| S2 |
| 1 |
| Sn |
| 11 |
| 9 |
| lim |
| n→∞ |
| 1 |
| S1 |
| 1 |
| S2 |
| 1 |
| Sn |
| 11 |
| 9 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com