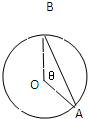某时钟的秒针端点A到中心点O的距离为5cm，秒针均匀地绕点O旋转，当时间t=0时，点A与钟面上标12的点B重合．
（1）将A，B两点间的直线距离d（cm）表示成时间t（s）的函数，其中t∈[0，60]；
（2）若h（t）=

5-d(60-20t)

，其中t∈[0，30]，求出函数h（t）的所有最高点坐标．

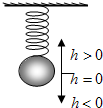如图所示，弹簧挂着的小球上下振动，时间t（s）与小球相对于平衡位置（即静止时的位置）的高度h（cm）之间的函数关系式为h=2sin(t+

π

4

)（t≥0），则小球往复振动一次的时间为（　　）

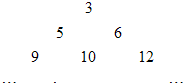（2013•江门二模）将集合{2^s+2^t|0≤s＜t且s，t∈Z}中的元素按上小下大，左小右大的顺序排成如图的三角形数表，将数表中位于第i行第j列的数记为b_ij（i≥j＞0），则b₆₅=．

（2012•肇庆二模）设函数f（x）=x³+ax²+bx（x＞0）的图象与直线y=4相切于M（1，4）．
（1）求y=f（x）在区间（0，4]上的最大值与最小值；
（2）是否存在两个不等正数s，t（s＜t），当s≤x≤t时，函数f（x）=x³+ax²+bx的值域是[s，t]，若存在，求出所有这样的正数s，t；若不存在，请说明理由．