下列判断语句正确的是（    ）

①对数式log_aN=b（a＞0且a≠1)和指数式a^b=N（a＞0且a≠1）是同一个关系式的两种不同表达形式②在同底条件下，对数式log_aN=b与指数式a^b=N可以互相转化③若a^b=N（a＞0且a≠1），则一定成立④对数的底数是任意正实数

A.①②           B.①②③④          C.①②③          D.④

给出下列命题：

    ①在研究身高和体重的关系时，求得相关指数R²≈0.64，可以叙述为“身高解释了64％的体重变化，而随机误差贡献了剩余的36％”，所以身高对体重的效应比随机误差的效应大得多．

    ②合情推理的结论不一定正确，在演绎推理中，只要前提和推理形式是正确的，结论必定是正确的．

    ③在回归分析模型中，残差平方和越小，说明模型的拟合效果越差．

    ④市政府调查江北水城市民收入与市民旅游欲望的关系时，抽查了3000人。经过计算发现K²=6.023，则，市政府有97.5％的把握认为市民收入与旅游欲望有关．其中正确命题的序号是____________.

随着工业化以及城市车辆的增加，城市的空气污染越来越严重，空气质量指数API一直居高不下，对人体的呼吸系统造成了严重的影响．现调查了某市500名居民的工作场所和呼吸系统健康，得到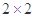列联表如下：

	室外工作	室内工作	合计
有呼吸系统疾病	150
无呼吸系统疾病		100
合计	200

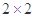（1）补全列联表；
（2）你是否有95%的把握认为感染呼吸系统疾病与工作场所有关；
（3）现采用分层抽样从室内工作的居民中抽取一个容量为6的样本，将该样本看成一个总体，从中随机的抽取两人，求两人都有呼吸系统疾病的概率．
参考公式与临界值表：K²＝

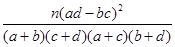
P(K2≥k0)	0．100	0．050	0．025	0．010	0．001
k0	2．706	3．841	5．024	6．635	10．828

已知函数f(x)=mx³+nx²(m、n∈R ,m≠0)的图像在（2，f(2)）处的切线与x轴平行.

（1）求n,m的关系式并求f(x)的单调减区间；

（2）证明：对任意实数0<x₁<x₂<1, 关于x的方程：

在（x₁,x₂）恒有实数解

（3）结合（2）的结论，其实我们有拉格朗日中值定理：若函数f(x)是在闭区间[a,b]上连续不断的函数，且在区间(a,b)内导数都存在，则在(a,b)内至少存在一点x₀，使得.如我们所学过的指、对数函数，正、余弦函数等都符合拉格朗日中值定理条件.试用拉格朗日中值定理证明：

当0<a<b时，（可不用证明函数的连续性和可导性）

给定有限个正数满足条件T:每个数都不大于50且总和L=1 275.现将这些数按下列要求进行分组,每组数之和不大于150且分组的步骤是:?

首先,从这些数中选择这样一些数构成第一组,使得150与这组数之和的差r₁与所有可能的其他选择相比是最小的,r₁称为第一组余差；?

然后,在去掉已选入第一组的数后,对余下的数按第一组的选择方式构成第二组,这时的余差为r₂；如此继续构成第三组(余差为r₃)、第四组(余差为r₄)、…,直至第N组(余差为r_n)把这些数全部分完为止.?

(1)判断r₁,r₂,…,r_n的大小关系,并指出除第N组外的每组至少含有几个数；?

(2)当构成第n(n＜N)组后,指出余下的每个数与r_n的大小关系,并证明

(3)对任何满足条件T的有限个正数,证明N≤11.