
题目列表(包括答案和解析)
| a2 |
| p |
| a3 |
| p2 |
| an-1 |
| pn-1 |
| an |
| pn-1 |
| 1+p |
| p |
| an |
| pn |
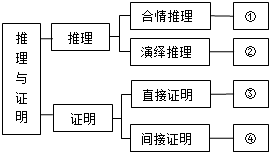 4、如图是人教A版教材选修1-2第二章“推理与证明”的知识结构图(部分),如果要加入知识点“三段论”,则应该放在图中( )
4、如图是人教A版教材选修1-2第二章“推理与证明”的知识结构图(部分),如果要加入知识点“三段论”,则应该放在图中( )| x |
| a |
| 1 |
| 2 |
| n |
 |
| k=1 |
| xk+1-xk |
| xk+2 |
| |||
| 2 |
 (文科做)已知点A1(2,0),A2(1,t),A3(0,b),A4(-1,t),A5(-2,0),其中t>0,b为正常数.
(文科做)已知点A1(2,0),A2(1,t),A3(0,b),A4(-1,t),A5(-2,0),其中t>0,b为正常数.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com