
题目列表(包括答案和解析)
| a |
| b |
| c |
| a |
| b |
| c |
| m |
| 1 |
| 2 |
| n |
| π |
| 6 |
| OQ |
| m |
| OP |
| n |
| a |
| b |
| a |
| b |
| m |
| 1 |
| 2 |
| n |
| π |
| 4 |
| OQ |
| m |
| OP |
| n |
| ||
| 2 |
| π |
| 4 |
| π |
| 2 |
(本题满分16分,第(1)小题6分,第(2)小题10分)
设 ,
, 定义一种向量的运算:
定义一种向量的运算: ,点P(x,y)在函数
,点P(x,y)在函数 的图像上运动,点Q在
的图像上运动,点Q在 的图像上运动,且满足
的图像上运动,且满足 (其中O为坐标原点)
(其中O为坐标原点)
(1)求函数f(x)的解析式;
(2)若函数 值域为
值域为 ,求a,b的值。
,求a,b的值。
设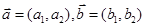 ,定义一种向量运算
,定义一种向量运算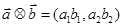 .已知
.已知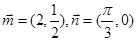 ,点
,点 在
在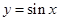 的图像上运动,点Q在
的图像上运动,点Q在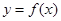 的图像上运动且满足
的图像上运动且满足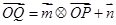 (其中O为坐标原点),则
(其中O为坐标原点),则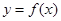 的最大值A及最小正周期T分别为(
)
的最大值A及最小正周期T分别为(
)
A.2,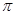 B.2,
B.2,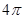 C.
C.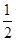 ,
,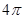 D.
D.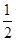 ,
,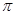
..(本小题满分14分)坐标法是解析几何中最基本的研究方法,坐标法是以坐标系为桥梁,把几何问题转化成代数问题,通过代数运算研究几何图形性质的方法.请利用坐标法解决以下问题:
(Ⅰ)在直角坐标平面内,已知 ,对任意
,对任意 ,试判断
,试判断 的形状;
的形状;
(Ⅱ)在平面内,已知 中,
中, ,
, 为
为 的中点,
的中点, 交
交 于
于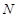 ,求证:
,求证: .
.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com