
题目列表(包括答案和解析)
(本小题满分12分)
已知某食品厂需要定期购买食品配料,该厂每天需要食品配料200千克,配料的价格为 元/千克,每次购买配料需支付运费236元.每次购买来的配料还需支付保管费用(若
元/千克,每次购买配料需支付运费236元.每次购买来的配料还需支付保管费用(若 天购买一次,需要支付
天购买一次,需要支付 天的保管费)。其标准如下: 7天以内(含7天),无论重量多少,均按10元/天支付;超出7天以外的天数,根据实际剩余配料的重量,以每天0.03元/千克支付.
天的保管费)。其标准如下: 7天以内(含7天),无论重量多少,均按10元/天支付;超出7天以外的天数,根据实际剩余配料的重量,以每天0.03元/千克支付.
(1)当9天购买一次配料时,求该厂用于配料的保管费用 是多少元?[
是多少元?[
(2)设该厂 天购买一次配料,求该厂在这
天购买一次配料,求该厂在这 天中用于配料的总费用
天中用于配料的总费用 (元)关于
(元)关于 的函数关系式,并求该厂多少天购买一次配料才能使平均每天支付的费用最少?
的函数关系式,并求该厂多少天购买一次配料才能使平均每天支付的费用最少?
(本小题满分12分)
已知某食品厂需要定期购买食品配料,该厂每天需要食品配料200千克,配料的价格为 元/千克,每次购买配料需支付运费236元.每次购买来的配料还需支付保管费用(若
元/千克,每次购买配料需支付运费236元.每次购买来的配料还需支付保管费用(若 天购买一次,需要支付
天购买一次,需要支付 天的保管费)。其标准如下: 7天以内(含7天),无论重量多少,均按10元/天支付;超出7天以外的天数,根据实际剩余配料的重量,以每天0.03元/千克支付.
天的保管费)。其标准如下: 7天以内(含7天),无论重量多少,均按10元/天支付;超出7天以外的天数,根据实际剩余配料的重量,以每天0.03元/千克支付.
(1)当9天购买一次配料时,求该厂用于配料的保管费用 是多少元?[
是多少元?[
(2)设该厂 天购买一次配料,求该厂在这
天购买一次配料,求该厂在这 天中用于配料的总费用
天中用于配料的总费用 (元)关于
(元)关于 的函数关系式,并求该厂多少天购买一次配料才能使平均每天支付的费用最少?
的函数关系式,并求该厂多少天购买一次配料才能使平均每天支付的费用最少?
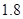 元/千克,每次购买配料需支付运费236元.每次购买来的配料还需支付保管费用(若
元/千克,每次购买配料需支付运费236元.每次购买来的配料还需支付保管费用(若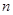 天购买一次,需要支付
天购买一次,需要支付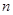 天的保管费)。其标准如下: 7天以内(含7天),无论重量多少,均按10元/天支付;超出7天以外的天数,根据实际剩余配料的重量,以每天0.03元/千克支付.
天的保管费)。其标准如下: 7天以内(含7天),无论重量多少,均按10元/天支付;超出7天以外的天数,根据实际剩余配料的重量,以每天0.03元/千克支付.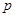 是多少元?[
是多少元?[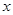 天购买一次配料,求该厂在这
天购买一次配料,求该厂在这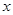 天中用于配料的总费用
天中用于配料的总费用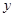 (元)关于
(元)关于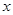 的函数关系式,并求该厂多少天购买一次配料才能使平均每天支付的费用最少?
的函数关系式,并求该厂多少天购买一次配料才能使平均每天支付的费用最少?(本小题满分9分)
已知函数![]() .
.
(1)求![]() 的单调减区间及
的单调减区间及![]() 图象的对称中心;
图象的对称中心;
(2)若![]() ,求
,求![]() 的最大值及取得最大值时
的最大值及取得最大值时![]() 的值.
的值.
(本小题满分14分)
某公司2009年9月投资14400万元购得上海世界博览会某种纪念品的专利权及生产设备,生产周期为一年.已知生产每件纪念品还需要材料等其它费用20元,为保证有一定的利润,公司决定纪念品的销售单价不低于150元,进一步的市场调研还发现:该纪念品的销售单价定在150元到250元之间较为合理(含150元及250元).并且当销售单价定为150元时,预测年销售量为150万件;当销售单价超过150元但不超过200元时,预测每件纪念品的销售价格每增加1元,年销售量将减少1万件;当销售单价超过200元但不超过250元时,预测每件纪念品的销售价格每增加1元,年销售量将减少1.2万件.
根据市场调研结果,设该纪念品的销售单价为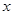 (元),年销售量为
(元),年销售量为 (万件),平均每件纪念品的利润为
(万件),平均每件纪念品的利润为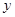 (元).
(元).
⑴求年销售量为 关于销售单价
关于销售单价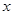 的函数关系式;
的函数关系式;
⑵该公司考虑到消费者的利益,决定销售单价不超过200元,问销售单价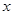 为多少时,平均每件纪念品的利润
为多少时,平均每件纪念品的利润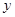 最大?
最大?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com