
题目列表(包括答案和解析)
(本题满分14分)已知数列![]() 中,
中,![]() 且点
且点![]() 在直线
在直线![]() 上. (1)求数列
上. (1)求数列![]() 的通项公式; (2)若函数
的通项公式; (2)若函数![]() 求函数
求函数![]() 的最小值; (3)设
的最小值; (3)设![]() 表示数列
表示数列![]() 的前项和.试问:是否存在关于
的前项和.试问:是否存在关于![]() 的整式
的整式![]() ,使得
,使得![]() 对于一切不小于2的自然数
对于一切不小于2的自然数![]() 恒成立? 若存在,写出
恒成立? 若存在,写出![]() 的解析式,并加以证明;若不存在,试说明理由.
的解析式,并加以证明;若不存在,试说明理由.
(本题满分14分)
已知数列![]() 中,
中,![]() 且点
且点![]() 在直线
在直线![]() 上.
上.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若函数![]() 求函数
求函数![]() 的最小值;
的最小值;
(3)设![]() 表示数列
表示数列![]() 的前
的前![]() 项和,
项和,
试证明:![]() .
.
(本题满分14分)已知函数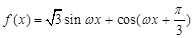


( ),且函数
),且函数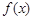 的最小正周期为
的最小正周期为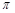 .
.
(Ⅰ)求函数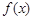 的解析式;
的解析式;
(Ⅱ)在△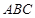 中,角
中,角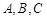 所对的边分别为
所对的边分别为 .若
.若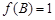 ,
,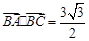 ,且
,且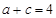 ,试求
,试求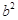 的值.
的值.
(本题满分14分,第(1)小题7分,第(2)小题7分)
某地发生特大地震和海啸,使当地的自来水受到了污染,某部门对水质检测后,决定往水中投放一种药剂来净化水质。已知每投放质量为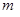 的药剂后,经过
的药剂后,经过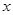 天该药剂在水中释放的浓度
天该药剂在水中释放的浓度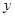 (毫克/升) 满足
(毫克/升) 满足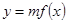 ,其中
,其中 ,当药剂在水中释放的浓度不低于
,当药剂在水中释放的浓度不低于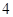 (毫克/升)时称为有效净化;当药剂在水中释放的浓度不低于
(毫克/升)时称为有效净化;当药剂在水中释放的浓度不低于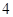 (毫克/升)
且不高于10(毫克/升)时称为最佳净化。
(毫克/升)
且不高于10(毫克/升)时称为最佳净化。
(1)如果投放的药剂质量为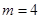 ,试问自来水达到有效净化一共可持续几天?
,试问自来水达到有效净化一共可持续几天?
(2)如果投放的药剂质量为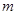 ,为了使在7天之内(从投放药剂算起包括7天)的自来水达到最佳净化,试确定应该投放的药剂质量
,为了使在7天之内(从投放药剂算起包括7天)的自来水达到最佳净化,试确定应该投放的药剂质量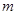 的值。
的值。
(本题满分14分,第(1)小题7分,第(2)小题7分)
某地发生特大地震和海啸,使当地的自来水受到了污染,某部门对水质检测后,决定往水中投放一种药剂来净化水质。已 知每投放质量为
知每投放质量为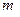 的药剂后,经过
的药剂后,经过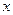 天该药剂在水中释放的浓度
天该药剂在水中释放的浓度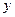 (毫克/升) 满足
(毫克/升) 满足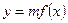 ,其中
,其中 ,当药剂在水中释放的浓度不低于
,当药剂在水中释放的浓度不低于 (毫克/升)时称为有效净化;当药剂在水中释放的浓度不低于
(毫克/升)时称为有效净化;当药剂在水中释放的浓度不低于 (毫克/升) 且不高于10(毫克/升)时称为最佳净化。
(毫克/升) 且不高于10(毫克/升)时称为最佳净化。
(1)如果投放的药剂质量为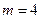 ,试问自来水达到有效净化一共可持续几天?
,试问自来水达到有效净化一共可持续几天?
(2)如果投放的药剂质量为 ,为了使在7天之内(从投放药剂算起包括7天)的自来水达到最佳净化,试确定应该投放的药剂质量
,为了使在7天之内(从投放药剂算起包括7天)的自来水达到最佳净化,试确定应该投放的药剂质量 的值。
的值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com