
题目列表(包括答案和解析)
.本小题满分12分)已知函数
 是R上的奇函数,
是R上的奇函数,
当 时
时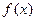 取得极值
取得极值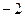 ,
,
(1)求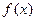 的单调区间和极大值;
的单调区间和极大值;
(2)证明对任意 ,不等式
,不等式 恒成立. 、
恒成立. 、
.(本小题满分13分)
已知数列 是其前
是其前 项和,且
项和,且 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设 是数列
是数列 的前
的前 项和
项和 ,求T10的值
,求T10的值
.(本小题满分14分)已知等比数列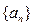 的公比为
的公比为 ,首项为
,首项为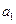 ,其前
,其前 项的和为
项的和为 .数列
.数列 的前
的前 项的和为
项的和为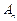 , 数列
, 数列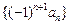 的前
的前 项的和为
项的和为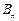
(Ⅰ)若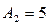 ,
,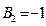 ,求
,求 的通项公式;(Ⅱ)①当
的通项公式;(Ⅱ)①当 为奇数时,比较
为奇数时,比较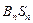 与
与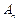 的大小; ②当
的大小; ②当 为偶数时,若
为偶数时,若 ,问是否存在常数
,问是否存在常数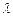 (与n无关),使得等式
(与n无关),使得等式 恒成立,若存在,求出
恒成立,若存在,求出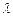 的值;若不存在,说明理由
的值;若不存在,说明理由
.本小题满分15分)
如图,已知椭圆E: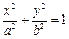
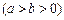 ,焦点为
,焦点为 、
、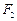 ,双曲线G:
,双曲线G: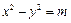
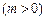 的顶点是该椭
的顶点是该椭 圆的焦点,设
圆的焦点,设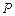 是双曲线G上异于顶点的任一点,直线
是双曲线G上异于顶点的任一点,直线 、
、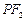 与椭圆的交点分别为A、B和C、D,已知三角形
与椭圆的交点分别为A、B和C、D,已知三角形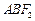 的周长等于
的周长等于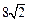 ,椭圆四个顶点组成的菱形的面积为
,椭圆四个顶点组成的菱形的面积为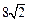 .
.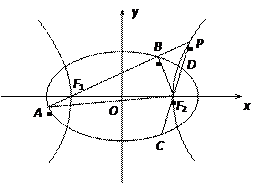
(1)求椭圆E与双曲线G的方程;
(2)设直线 、
、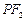 的斜率分别为
的斜率分别为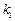 和
和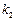 ,探求
,探求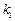 和
和
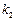 的关系;
的关系;
(3)是否存在常数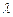 ,使得
,使得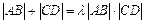 恒成立?
恒成立?
若存在,试求出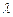 的值;若不存在, 请说明理由.
的值;若不存在, 请说明理由.
.( 本小题满分13分)
本小题满分13分)
某慈善机构举办一次募捐演出,有一万人参加,每人一张门票,每张100元. 在演出过程中穿插抽奖活动.第一轮抽奖从这一万张票根中随机抽取10张,其持有者获得价值1000元的奖品,并参加第二轮抽奖活动.第二轮抽奖由第一轮获奖者独立操作按钮,电脑随机产生两个数 ,
, (
( ,
, ),随即按如右所示程序框图运行相应程序.若电脑显示“中奖”,则抽奖者获得9000元奖金;若电脑显示“谢谢”,则不中奖.
),随即按如右所示程序框图运行相应程序.若电脑显示“中奖”,则抽奖者获得9000元奖金;若电脑显示“谢谢”,则不中奖.
(Ⅰ)已知小曹在第一轮抽奖中被抽中,
求小曹在第二轮抽奖中获奖的概率;
(Ⅱ)若小叶参加了此次活动,求小叶参加此次活动收益的期望;
(Ⅲ)若此次募捐除奖品和奖金外,不计其它支出,该机构想获得96万元的慈善款.问该慈善机构此次募捐 是否能达到预期目标.
是否能达到预期目标.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com