
题目列表(包括答案和解析)
(本题满分14分)
下表提供了某厂节油降耗技术发行后生产甲产品过程中记录的产量 (吨)与相应的生
(吨)与相应的生
产能耗y(吨标准煤)的几组对应数据.
|
x |
3 |
4 |
5 |
6 |
|
y |
2.5 |
3 |
4 |
4.5 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程y= ;
;
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤,试根据(2)求出的线性
回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)
(本题满分14分) 已知函数
(I)若 在其定义域是增函数,求b的取值范围;
在其定义域是增函数,求b的取值范围;
(II)在(I)的结论下,设函数 的最小值;
的最小值;
(III)设函数 的图象C1与函数
的图象C1与函数 的图象C2交于点P、Q,过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N,问是否存在点R,使C1在M处的切线与C2在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由.
的图象C2交于点P、Q,过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N,问是否存在点R,使C1在M处的切线与C2在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由.
(本题满分14分)
抛物线D以双曲线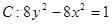 的焦点
的焦点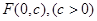 为焦点.
为焦点.
(1)求抛物线D的标准方程;
(2)过直线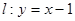 上的动点P作抛物线D的两条切线,切点为A,B.求证:直线AB过定点Q,并求出Q的坐标;
上的动点P作抛物线D的两条切线,切点为A,B.求证:直线AB过定点Q,并求出Q的坐标;
(3)在(2)的条件下,若直线PQ交抛物线D于M,N两点,求证:|PM|·|QN|=|QM|·|PN|
(本题满分14分)
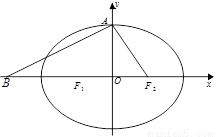
设椭圆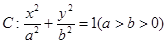 的左、右焦点分别为
的左、右焦点分别为 ,上顶点为
,上顶点为 ,在
,在 轴负半轴上有一点
轴负半轴上有一点 ,满足
,满足 ,且
,且 .
.
(1)求椭圆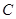 的离心率;
的离心率;
(2)若过 三点的圆恰好与直线
三点的圆恰好与直线 相切,求椭圆
相切,求椭圆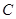 的方程;
的方程;
(3)在(2)的条件下,过右焦点 作斜率为
作斜率为 的直线
的直线 与椭圆
与椭圆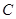 交于
交于 两点,在
两点,在 轴上是否存在点
轴上是否存在点 使得以
使得以 为邻边的平行四边形是菱形,如果存在,求出
为邻边的平行四边形是菱形,如果存在,求出 的取值范围,如果不存在,说明理由。
的取值范围,如果不存在,说明理由。
(本题满分14分)某种储蓄按复利(把前一期的利息和本金加在一起作本金,再计算下一期的利息)计算利息,若本金为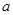 元,每期利率为
元,每期利率为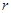 ,设存期为
,设存期为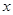 ,本利和(本金加上利息)为
,本利和(本金加上利息)为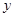 元。
元。
(Ⅰ)写出本利和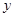 随存期
随存期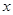 变化的函数解析式;
变化的函数解析式;
(Ⅱ)如果存入本金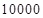 元,每期利率为
元,每期利率为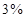 ,试计算
,试计算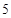 期后的本利和。
期后的本利和。
(参考数据: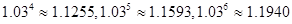 )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com