
题目列表(包括答案和解析)
(本小题满分16分)
设![]() 是定义在区间
是定义在区间![]() 上的函数,其导函数为
上的函数,其导函数为![]() 。如果存在实数
。如果存在实数![]() 和函数
和函数![]() ,其中
,其中![]() 对任意的
对任意的![]() 都有
都有![]() >0,使得
>0,使得![]() ,则称函数
,则称函数![]() 具有性质
具有性质![]() 。
。
(1)设函数![]()
![]() ,其中
,其中![]() 为实数。
为实数。
(i)求证:函数![]() 具有性质
具有性质![]() ; (ii)求函数
; (ii)求函数![]() 的单调区间。
的单调区间。
(2)已知函数![]() 具有性质
具有性质![]() 。给定
。给定![]() 设
设![]() 为实数,
为实数,
![]() ,
,![]() ,且
,且![]() ,
,
若|![]() |<|
|<|![]() |,求
|,求![]() 的取值范围。
的取值范围。
(本小题满分16分)已知函数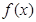 =
=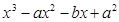 ,
,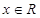 ,
,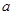 ,
,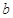 为常数。
为常数。
(1)若函数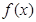 在
在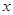 =1处有极值10,求实数
=1处有极值10,求实数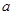 ,
,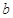 的值;
的值;
(2)若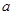 =0,(I)方程
=0,(I)方程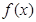 =2在
=2在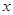 ∈[-4,4]上恰有3个不相等的实数解,求实数
∈[-4,4]上恰有3个不相等的实数解,求实数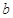 的取值范围;(II)不等式
的取值范围;(II)不等式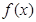 +2
+2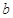 ≥0对
≥0对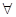
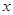 ∈[1,4]恒成立,求实数
∈[1,4]恒成立,求实数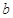 的取值范围。
的取值范围。
(本题满分16分)
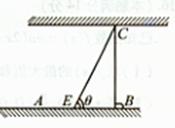
如图为河岸一段的示意图,一游泳者站在河岸的A点处,欲前往河对岸的C点处。若河宽BC为100m,A、B相距100m,他希望尽快到达C,准备从A步行到E(E为河岸AB上的点),再从E游到C。已知此人步行速度为v,游泳速度为0.5v。
(I)设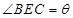 ,试将此人按上述路线从A到C所需时间T表示为
,试将此人按上述路线从A到C所需时间T表示为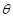 的函数;并求自变量
的函数;并求自变量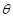 取值范围;
取值范围;
II)当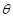 为何值时,此人从A经E游到C所需时间T最小,其最小值是多少?
为何值时,此人从A经E游到C所需时间T最小,其最小值是多少?
 ,试将此人按上述路线从A到C所需时间T表示为
,试将此人按上述路线从A到C所需时间T表示为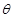 的函数;并求自变量
的函数;并求自变量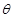 取值范围;
取值范围;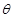 为何值时,此人从A经E游到C所需时间T最小,其最小值是多少?
为何值时,此人从A经E游到C所需时间T最小,其最小值是多少?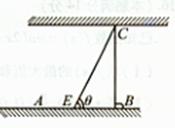
、(本小题满分16分)已知a,b是实数,函数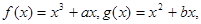
 和
和 是
是 的导函数,若
的导函数,若 在区间I上恒成立,则称
在区间I上恒成立,则称 和
和 在区间I上单调性一致
在区间I上单调性一致
(1)设 ,若函数
,若函数 和
和 在区间
在区间 上单调性一致,求实数b的取值范围;
上单调性一致,求实数b的取值范围;
(2)设 且
且 ,若函数
,若函数 和
和 在以a,b为端点的开区间上单调性一致,求|a-b|的最大值。
在以a,b为端点的开区间上单调性一致,求|a-b|的最大值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com