(本小题满分12分) 求满足下列条件的椭圆的标准方程．

    （1）焦点在坐标轴上，且经过两点；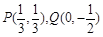

    （2）经过点（2，－3）且与椭圆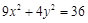具有共同的焦点．

（本小题满分12分）

设函数，其中是某范围内的随机数，分别在下列条件下，求事件A “且”发生的概率.

 （Ⅰ）若随机数；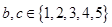

    （Ⅱ）已知随机函数产生的随机数的范围为, 是算法语句和的执行结果．(注: 符号“”表示“乘号”)

（本题满分12分）在直角坐标平面中，△的两个顶点的坐标分别为，，平面内两点同时满足下列条件：①=0；②；③∥（1）求△的顶点的轨迹方程；（2）过点直线与（1）中轨迹交于不同的两点，求△面积的最大值.

(本小题满分12分)对于定义域为D的函数，若同时满足下列条件：①在D内单调递增或单调递减；②存在区间[]，使在[]上的值域为[]；那么把（）叫闭函数。（1）求闭函数符合条件②的区间[]；

（2）判断函数是否为闭函数？并说明理由；

（3）判断函数是否为闭函数？若是闭函数，求实数的取值范围。

（04年北京卷）(12分)

给定有限正数满足条件T: 每个数都不大于50且总和L=1275.现将这些数按下列要求进行分组,每组数之和不大于150且分组的步骤是:

首先,从这些数中选择这样一些数构成第一组,使得150与这组数之和的差r₁与所有可能的其他选择相比是最小的,r₁称为第一组余差;

然后,在去掉已选入第一组的数后,对余下的数按第一组的选择方式构成第二组,这时的余差r₂;如此继续构成第三组(余差为r₃)、第四组（余差为r₄）、…，直至第N组（余差为r_N）把这些数全部分完为止。

(Ⅰ) 判断r₁,r₂,…，r_N的大小关系，并指出除第N组外的每组至少含有几个数；

(Ⅱ) 当构成n(n>N)组后，指出余下的每个数与r_n的大小关系，并证明

  ；

（Ⅲ）对任何满足条件T的有限个正数，证明：N≤11。