
题目列表(包括答案和解析)
 和
和 为直角坐标第xOy中与x轴和y轴正方向相同的单位向量,根据平面向量基本定理,对于该平面上的任意一个向量
为直角坐标第xOy中与x轴和y轴正方向相同的单位向量,根据平面向量基本定理,对于该平面上的任意一个向量 ,则存在唯一的一对实数λ,μ,使得
,则存在唯一的一对实数λ,μ,使得 =
= +μ
+μ ,我们就把实数对(λ,μ)称作向量
,我们就把实数对(λ,μ)称作向量 的坐标.并依据这样的定义研究了向量加法、减法、数乘向量及数量积的坐标运算公式.现在我们用
的坐标.并依据这样的定义研究了向量加法、减法、数乘向量及数量积的坐标运算公式.现在我们用 和
和 表示斜坐标系x‘Oy’中与x‘轴和y轴正方向相同的单位向量,其中<
表示斜坐标系x‘Oy’中与x‘轴和y轴正方向相同的单位向量,其中< ,
, >=
>= ,
, 和
和 做基底向量定义斜坐标系x‘Oy’平面上的任意一个向量
做基底向量定义斜坐标系x‘Oy’平面上的任意一个向量 的坐标;
的坐标; 和
和 为直角坐标第xOy中与x轴和y轴正方向相同的单位向量,根据平面向量基本定理,对于该平面上的任意一个向量
为直角坐标第xOy中与x轴和y轴正方向相同的单位向量,根据平面向量基本定理,对于该平面上的任意一个向量 ,则存在唯一的一对实数λ,μ,使得
,则存在唯一的一对实数λ,μ,使得 =
= +μ
+μ ,我们就把实数对(λ,μ)称作向量
,我们就把实数对(λ,μ)称作向量 的坐标.并依据这样的定义研究了向量加法、减法、数乘向量及数量积的坐标运算公式.现在我们用
的坐标.并依据这样的定义研究了向量加法、减法、数乘向量及数量积的坐标运算公式.现在我们用 和
和 表示斜坐标系x‘Oy’中与x‘轴和y轴正方向相同的单位向量,其中<
表示斜坐标系x‘Oy’中与x‘轴和y轴正方向相同的单位向量,其中<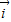 ,
, >=
>= ,
,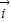 和
和 做基底向量定义斜坐标系x‘Oy’平面上的任意一个向量
做基底向量定义斜坐标系x‘Oy’平面上的任意一个向量 的坐标;
的坐标;选择题:
(1)
如果a,b是两个单位向量,那么下列四个结论中正确的是[
]|
(A)a =b |
(B)a ·b=1 |
|
(C) |
(D) |
(2)
对于任意向量a、b,下列命题中正确的是[
](A)
若a,b满足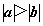 ,且a与b同向,则a>b
,且a与b同向,则a>b
(B)
(C)
(D)
(3)在四边形ABCD中,若 ,则
,则
[
]|
(A)ABCD 是矩形 |
(B)ABCD 是菱形 |
|
(C)ABCD 是正方形 |
(D)ABCD 是平行四边形 |
(4)
设a是非零向量,λ是非零实数,下列结论中正确的是[
]|
(A)a 与-λa的方向相反 |
(B) |
|
(C)a 与 的方向相同 的方向相同 |
(D) |
(5)
设M是□ABCD的对角线的交点,O为任意一点,则 等于
等于
[
]|
(A) |
(B)2 |
(C)3 |
(D)4 |
(6)
下列各组向量中,可以作为基底的是[
](A)
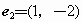
(B)
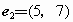
(C)
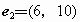
(D)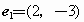

| e1 |
| e2 |
| a |
| a |
| e1 |
| e2 |
| a |
| i |
| j |
| i |
| j |
| π |
| 3 |
| i |
| j |
| a |
| e1 |
| e2 |
| a |
| a |
| e1 |
| e2 |
| a |
| i |
| j |
| i |
| j |
| π |
| 3 |
| i |
| j |
| a |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com