
题目列表(包括答案和解析)
(08年上海卷文)(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
已知数列![]() :
:![]() ,
,![]() ,
,![]() ,
,![]() (
(![]() 是正整数),与数列
是正整数),与数列
![]() :
:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (
(![]() 是正整数).
是正整数).
记![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)求证:当![]() 是正整数时,
是正整数时,![]() ;
;
(3)已知![]() ,且存在正整数
,且存在正整数![]() ,使得在
,使得在![]() ,
,![]() ,
,![]() ,
,![]() 中有4项为100.
中有4项为100.
求![]() 的值,并指出哪4项为100.
的值,并指出哪4项为100.
(本题满分14分) 本题共有2个小题,第1小题满分6分,第2小题满分8分.
(理)某种型号汽车四个轮胎半径相同,均为 ,同侧前后两轮胎之间的距离(指轮胎中心之间距离)为
,同侧前后两轮胎之间的距离(指轮胎中心之间距离)为 (假定四个轮胎中心构成一个矩形). 当该型号汽车开上一段上坡路
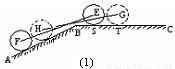
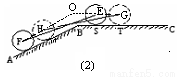
(假定四个轮胎中心构成一个矩形). 当该型号汽车开上一段上坡路 (如图(1)所示,其中
(如图(1)所示,其中 (
(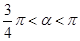 )),且前轮
)),且前轮 已在
已在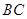 段上时,后轮中心在
段上时,后轮中心在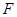 位置;若前轮中心到达
位置;若前轮中心到达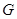 处时,后轮中心在
处时,后轮中心在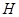 处(假定该汽车能顺利驶上该上坡路). 设前轮中心在
处(假定该汽车能顺利驶上该上坡路). 设前轮中心在 和
和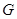 处时与地面的接触点分别为
处时与地面的接触点分别为 和
和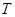 ,且
,且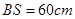 ,
,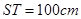 . (其它因素忽略不计)
. (其它因素忽略不计)
(1)如图(2)所示,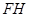 和
和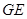 的延长线交于点
的延长线交于点 ,
,
求证: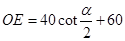 (cm);
(cm);
(2)当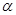 =
=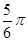 时,后轮中心从
时,后轮中心从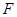 处移动到
处移动到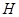 处实际移动了多少厘米? (精确到1cm)
处实际移动了多少厘米? (精确到1cm)
(本题满分8分)
如图,在正方体 中,
中,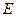 是
是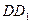 的中点,
的中点,
求证: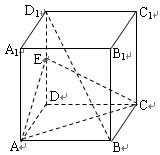
(1)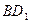 ∥平面
∥平面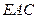 ;
;
(2)求异面直线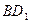 与
与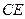 所成角的余弦值.
所成角的余弦值.
(文)(本小题8分)
如图,在四棱锥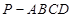 中,
中, 平面
平面 ,
, ,
, ,
,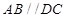 ,
,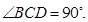
(1)求证: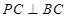 ;
;
(2)求点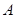 到平面
到平面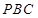 的距离
的距离
证明:(1) 平面
平面 ,
,
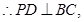 又
又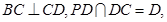
 平面
平面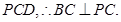 (4分)
(4分)
(2)设点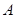 到平面
到平面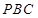 的距离为
的距离为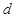 ,
,
 ,
, ,
,
求得 即点
即点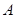 到平面
到平面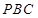 的距离为
的距离为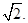 (8分)
(8分)
(其它方法可参照上述评分标准给分)
(本题8分)已知等差数列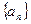 满足:
满足: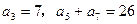 ,
,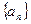 的前
的前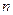 项和为
项和为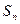 。
。
(1)求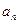 及
及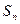 ;
;
(2)令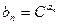 (其中
(其中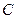 为常数,且
为常数,且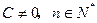 ),求证数列
),求证数列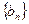 为等比数列。
为等比数列。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com