
(本题满分14分) 本题共有2个小题,第1小题满分6分,第2小题满分8分.
(理)某种型号汽车四个轮胎半径相同,均为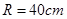 ,同侧前后两轮胎之间的距离(指轮胎中心之间距离)为
,同侧前后两轮胎之间的距离(指轮胎中心之间距离)为 (假定四个轮胎中心构成一个矩形). 当该型号汽车开上一段上坡路
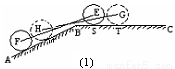
(假定四个轮胎中心构成一个矩形). 当该型号汽车开上一段上坡路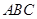 (如图(1)所示,其中
(如图(1)所示,其中 (
( )),且前轮
)),且前轮 已在
已在 段上时,后轮中心在
段上时,后轮中心在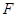 位置;若前轮中心到达
位置;若前轮中心到达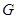 处时,后轮中心在
处时,后轮中心在 处(假定该汽车能顺利驶上该上坡路). 设前轮中心在
处(假定该汽车能顺利驶上该上坡路). 设前轮中心在 和
和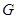 处时与地面的接触点分别为
处时与地面的接触点分别为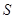 和
和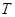 ,且
,且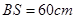 ,
,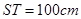 . (其它因素忽略不计)
. (其它因素忽略不计)
(1)如图(2)所示,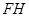 和
和 的延长线交于点
的延长线交于点 ,
,
求证: (cm);
(cm);

(2)当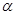 =
=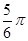 时,后轮中心从
时,后轮中心从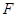 处移动到
处移动到 处实际移动了多少厘米? (精确到1cm)
处实际移动了多少厘米? (精确到1cm)
(1)由OE//BC,OH//AB,得∠EOH= ,
,

过点B作BM⊥OE,BN⊥OH,则Rt OMB
OMB Rt
Rt ONB,从而∠BOM=
ONB,从而∠BOM= .
.
在Rt OMB中,由BM=40得OM=40cot
OMB中,由BM=40得OM=40cot ,从而,OE=OM+ME=OM+BS=
,从而,OE=OM+ME=OM+BS= .
.
(2)98cm。
【解析】
试题分析:(1) 由OE//BC,OH//AB,得∠EOH= ,
2分
,
2分

过点B作BM⊥OE,BN⊥OH,则
Rt OMB
OMB Rt
Rt ONB,从而
ONB,从而
∠BOM= . 4分
. 4分
在Rt OMB中,由BM=40得OM=40cot
OMB中,由BM=40得OM=40cot ,从而,OE=OM+ME=OM+BS=
,从而,OE=OM+ME=OM+BS= . 6分
. 6分
(2)由(1)结论得OE= .
.
设OH=x,OF=y,
在 OHG中,由余弦定理得,
OHG中,由余弦定理得,
2802=x2+( +100)2-2x(
+100)2-2x( +100)cos1500 ,
+100)cos1500 ,
解得x 118.8cm.
9分
118.8cm.
9分
在 OEF中,由余弦定理得,
OEF中,由余弦定理得,
2802=y2+( )2-2y(
)2-2y( )cos1500 ,
)cos1500 ,
解得y 216.5cm.
12分
216.5cm.
12分
所以,FH=y-x 98cm,
98cm,
即后轮中心从F处移动到H处实际移动了约98cm. 14分
考点:正弦定理;余弦定理;解三角形的实际应用。
点评:在解应用题时,我们要分析题意,分清已知与所求,再根据题意正确画出示意图,通过这一步可将实际问题转化为可用数学方法解决的问题。解题中,要注意正、余弦定理的灵活应用。


科目:高中数学 来源: 题型:
| π |
| 3 |
|
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分14分)如图,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,![]() 为
为![]() 上的点,且BF⊥平面ACE.
上的点,且BF⊥平面ACE.
(1)求证:AE⊥BE;(2)求三棱锥D-AEC的体积;(3)设M在线段AB上,且满足AM=2MB,试在线段CE上确定一点N,使得MN∥平面DAE.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省高三上学期期中考试数学 题型:解答题
(本题满分14分)已知集合A={x|x2-2x-3≤0,x∈R},B={x|x2-2mx+m2-4≤0,x∈R,m∈R}
(Ⅰ)若A B=[0,3],求实数m的值
B=[0,3],求实数m的值
(Ⅱ)若A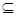 CRB,求实数m的取值范围
CRB,求实数m的取值范围
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省高三上学期第三次月考理科数学卷 题型:解答题
(本题满分14分)
已知点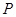 是⊙
是⊙ :
: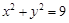 上的任意一点,过
上的任意一点,过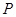 作
作 垂直
垂直 轴于
轴于 ,动点
,动点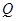 满足
满足 。
。
(1)求动点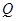 的轨迹方程;
的轨迹方程;
(2)已知点 ,在动点
,在动点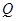 的轨迹上是否存在两个不重合的两点
的轨迹上是否存在两个不重合的两点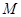 、
、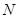 ,使
,使 (O是坐标原点),若存在,求出直线
(O是坐标原点),若存在,求出直线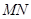 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源:2014届江西省高一第二学期入学考试数学 题型:解答题
(本题满分14分)已知函数 .
.
(1)求函数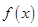 的定义域;
的定义域;
(2)判断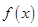 的奇偶性;
的奇偶性;
(3)方程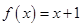 是否有根?如果有根
是否有根?如果有根 ,请求出一个长度为
,请求出一个长度为 的区间
的区间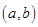 ,使
,使

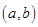 ;如果没有,请说明理由?(注:区间的长度为
;如果没有,请说明理由?(注:区间的长度为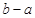 ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com