
题目列表(包括答案和解析)
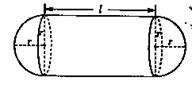
(本小题满分13分).某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为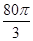 立方米,且
立方米,且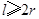 .假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为
.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为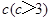 千元,设该容器的建造费用为
千元,设该容器的建造费用为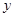 千元.
千元.
(Ⅰ)写出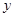 关于
关于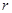 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域;
(Ⅱ)求该容器的建造费用最小时的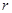 .
.
(本小题满分13分).某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为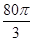 立方米,且
立方米,且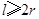 .假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为
.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为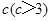 千元,设该容器的建造费用为
千元,设该容器的建造费用为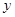 千元.
千元.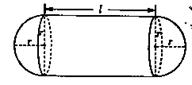
(Ⅰ)写出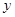 关于
关于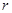 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域;
(Ⅱ)求该容器的建造费用最小时的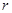 .
.
(本小题满分13分)随着石油资源的日益紧缺,我国决定建立自己的石油储备基地,
已知某石油储备基地原储有石油![]() 吨,按计划正式运营后的第一年进油量为已储油量的25%,以后每年的进油量均为上一年底储油量的25%,且每年年内用出
吨,按计划正式运营后的第一年进油量为已储油量的25%,以后每年的进油量均为上一年底储油量的25%,且每年年内用出![]() 吨,设
吨,设![]() 为正式运营后第
为正式运营后第![]() 年年底的石油储量.(Ⅰ)求
年年底的石油储量.(Ⅰ)求![]() 、
、![]() 、
、![]() ; (Ⅱ)猜测出
; (Ⅱ)猜测出![]() 的表达式并用数学归纳法予以证明;(Ⅲ)为抵御突发事件,该油库年底储油量不得少于
的表达式并用数学归纳法予以证明;(Ⅲ)为抵御突发事件,该油库年底储油量不得少于![]() 吨,如果
吨,如果![]() 吨,该油库能否长期按计划运营?如果能,请加以证明;如果不能,请说明理由.(计算中可供参考的数据:
吨,该油库能否长期按计划运营?如果能,请加以证明;如果不能,请说明理由.(计算中可供参考的数据:![]() ,
,![]() )
)
(本小题满分13分)
已知等差数列 的公差为
的公差为 ,前
,前 项和为
项和为 ,且满足
,且满足 ,
,
(1)试用 表示不等式组
表示不等式组 ,并在给定的坐标系中画出不等式组表示的平面区域;
,并在给定的坐标系中画出不等式组表示的平面区域;
(2)求 的最大值,并指出此时数列
的最大值,并指出此时数列 的公差
的公差 的值.
的值. [
[
(本小题满分13分)
已知函数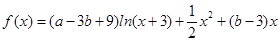 .
.
(1)当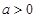 且
且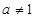 ,
,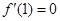 时,试用含
时,试用含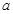 的式子表示
的式子表示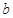 ,并讨论
,并讨论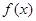 的单调区间;
的单调区间;
(2)若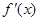 有零点,
有零点,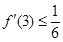 ,且对函数定义域内一切满足
,且对函数定义域内一切满足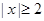 的实数
的实数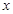 有
有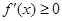 .
.
①求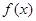 的表达式;
的表达式;
②当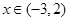 时,求函数
时,求函数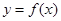 的图象与函数
的图象与函数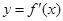 的图象的交点坐标.
的图象的交点坐标.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com