
题目列表(包括答案和解析)
已知函数 ,数列
,数列 的项满足:
的项满足: ,(1)试求
,(1)试求
(2) 猜想数列 的通项,并利用数学归纳法证明.
的通项,并利用数学归纳法证明.
【解析】第一问中,利用递推关系 ,
, 
 ,
, 
第二问中,由(1)猜想得: 然后再用数学归纳法分为两步骤证明即可。
然后再用数学归纳法分为两步骤证明即可。
解: (1)  ,
,

 ,
,  …………….7分
…………….7分
(2)由(1)猜想得:
(数学归纳法证明)i)  ,
,
 ,命题成立
,命题成立
ii) 假设 时,
时, 成立
成立
则 时,
时,


综合i),ii) :  成立
成立
已知函数![]() 定义在区间
定义在区间![]() ,对任意
,对任意![]() ,恒有
,恒有
![]() 成立,又数列
成立,又数列![]() 满足
满足![]()
(I)在(-1,1)内求一个实数t,使得![]()
(II)求证:数列![]() 是等比数列,并求
是等比数列,并求![]() 的表达式;
的表达式;
(III)设![]() ,是否存在
,是否存在![]() ,使得对任意
,使得对任意![]() ,
,![]() 恒成立?若存在,求出m的最小值;若不存在,请说明理由。
恒成立?若存在,求出m的最小值;若不存在,请说明理由。
已知函数 的图象经过坐标原点,且
的图象经过坐标原点,且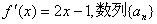 的前
的前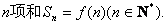
(I)求数列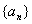 的通项公式;
的通项公式;
(II)若数列 满足
满足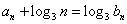 ,求数列
,求数列 的前n项和。
的前n项和。
(Ⅲ)设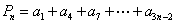 ,
,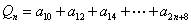 ,其中
,其中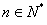 ,试比较
,试比较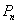 与
与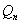 的大小,并证明你的结论。
的大小,并证明你的结论。
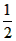 )=1,且满足x,y∈(-1,1)时有
)=1,且满足x,y∈(-1,1)时有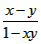 ),数列{xn}满足
),数列{xn}满足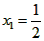 ,
,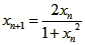
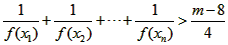 恒成立?若存在,求出m的最大值。
恒成立?若存在,求出m的最大值。
已知函数 当
当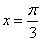 时,
时,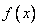 取得极小值
取得极小值 。
。
(1) 求 的值;
的值;
(2) 设直线 ,曲线
,曲线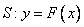 ,若直线
,若直线 与曲线
与曲线 同时满足下列两个条件:
同时满足下列两个条件:
(i) 直线 与曲线
与曲线 相切且至少有两个切点;
相切且至少有两个切点;
(ii) 对任意 都有
都有 ,则称直线
,则称直线 为曲线
为曲线 的“上夹线”。试证明:直线
的“上夹线”。试证明:直线 是曲线
是曲线 的“上夹线”。
的“上夹线”。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com